本文的提出了全参数时间复杂度(Full parameter time complexity，以下简称FPTC)，它考虑了所有可能耗时的参数。同时，我们定义了一个系数$\omega$来模拟不同分类器在不同平台之间的物理差异。
在下面的章节中，我们将根据FPTC在本文中的定义，具体推导以下几个算法的FPTC，其中包括：$k$NN ($k$-nearest neighbors) , LR (logistic regression) , CART (classification and regression tree) , RF (random forest)和 SVM (support vector machine) 。为了检验FPTC和相应的系数$\omega$的有效性，我们选择了新疆维吾尔自治区和Sentinel-2A数据集作为案例研究。
本文将首先阐述FPTC的定义，然后推导常用几个算法的FPTC，随后在具体的数据集中，验证我们提出的FPTC的有效性，同时进一步研究相关参数的影响。

原文链接

Zheng, X., Jia, J., Guo, S., Chen, J., Sun, L., Xiong, Y., & Xu, W. (2021). Full Parameter Time Complexity (FPTC): A Method to Evaluate the Running Time of Machine Learning Classifiers for Land Use/Land Cover Classification. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 14, 2222–2235. https://doi.org/10.1109/JSTARS.2021.3050166

算法时间估算的基本理论

对自然灾害和风险的评估是从公众到政府应急管理人员等各种行为者决策过程的基础。迅速量化损失和预期的未来损失通常是了解当前情况的第一步。遥感影像的土地利用/土地覆盖 (Land use/land cover, 以下简称LULC) 产品可以为这一目的提供第一手信息 。由于这一决策过程通常是紧迫的，在有限的时间和资源下选择合适的分类算法来实现这一目标可能是具有挑战性的引用。除了分类精度之外，算法的实际时间消耗是运行任务之前需要仔细评估的另一个方面 （Donoho2012,Huang2017,Khatami2016）。在没有准确预测时间消耗的情况下，在这些紧急情况下选择LULC分类算法可能是盲目的和主观的。

通常，估计分类任务的时间消耗的方法可以分为两类：(1) 基于采样数据的方法和；(2) 基于时间复杂度的方法。第一类包括基于运行程序和启动对采样数据集的时间计算功能进行估计。这方法是假定样本和整个数据集之间的实际运行时间可以通过线性或非线性关系来简化。虽然这些方法被用于各种研究，但是它们的缺点是：(1) 这种线性或非线性关系高度依赖于硬件，不能在不同的计算环境中推广；(2) 算法的不同参数 (操作参数和隐藏参数) 的影响被视为一个黑匣子。同时，这些参数对运行时间的影响尚不清楚。第二类涉及基于时间复杂性分析的评估。常用的渐近时间复杂度就属于这一类，通常称为传统时间复杂度 (Traditional time complexity，以下简称TTC)。TTC是输入大小(例如，样本数量)的函数，它衡量在单位操作迭代(例如，加法或乘法)下，随着输入大小的增加，计算复杂度的变化。假定每个单元操作的时间具有相同的值，因此可以估计迭代次数与运行时间成比例。在计算TTC的过程中，忽略了许多低阶细节。例如，当我们计算函数 $f\left(n\right)=an^2+bn+c$ 的TTC时(
其中$n$ 代表了输入规模)，我们只关心$n$的最高次项，即 $f\left(n\right)=n^2$ 。$O(n^2)$ 表示了这个函数的时间复杂度的最上界。 TTC的目的是在理论级别捕获随着数据大小的增加而加速的运行时间 $({N})$。然而， 这很难用于运行时间的准确预测，特别是在遥感LULC分类任务中，时间消耗不仅与数据大小$({N})$有关，还与其他参数有关（例如，波段数或者SVM中支持向量的个数）。 如何考虑这些参数的影响来预测总体时间消耗仍然是一个挑战。

事实上，在不考虑不同平台(如CPU和GPU)之间的物理差异的情况下，分类算法的时间消耗会受到：(1) 数据大小; (2) 类的数量；(3) 波段/特征的数量; (4) 算法的迭代结构; (5) 算法的操作参数(如随机森林中的树的数量)和 (6) 算法的隐藏参数(如支持向量的数量)的影响。所有这些组件都通过未知机制以不同的方式影响算法的实际时间消耗。确定如何量化每个部分的贡献是预测实际时间的关键。

基于FPTC进行时间估算的基础理论与常见算法FPTC的推导

FPTC 包含了两个部分：一部分为 $F(n,m,v,\boldsymbol{\theta}’)$，这个部分与算法息息相关，可以根据对特定分类器的结构分析得出。这个部分是关于 $n,m,v$ 和 $\boldsymbol{\theta}’$的函数。其中，$n$ 为样本量大小， $m$ 为类别数， $v$ 为波段数， $\boldsymbol{\theta}’$ 代表与算法相关的参数合集。值得注意的是不同算法的 $\boldsymbol{\theta}’$ 可能是不一样的。举个例子， $k$NN 的 $\boldsymbol{\theta}’$ 可能包含了最近邻数 $u$, 而SVM的$\boldsymbol{\theta}’$可能包含了迭代次数$Q$和支持向量个数$k$。第二个部分是参数$\omega $, 它是反映计算环境因素的物理相关部分对运行时间的影响, 例如CPU/GPU或者RAM的速度。因此，系数 $\omega $与运行平台息息相关。通常，在数据集的一小部分上进行预实验可以帮助我们评估特定分类器的这个系数。结合这两个部分，FPTC的定义如下：

\[t^*= F(n,m,v,\boldsymbol{\theta}')\] \[t'= \omega \times t^*\]

$t’\ $表示真实的运行时间， $\omega$ 表示系数， $\ t^*\ $是通过分析算法结构儿预估的时间。在下一节中，我们将推导出遥感领域中五种经典和常用的分类器的FPTC算法相关部分。我们按以下顺序推导出所选算法的FPTC： $k$NN，LR，CART，RF和 SVM。

$k$NN的FPTC推导

$k$NN分类器是一个懒惰的学习器，这意味着建立模型的时间成本很低，但对测试样本进行分类的时间成本相对较高。为了计算测试样本的时间复杂度，我们将$k$NN分类器的FPTC分解为两部分来说明。首先，计算训练样本$\textbf{x}^{(e)}$ 和测试数据之间的距离的FPTC为$F(v)$。当训练集有$n$个样本时，FPTC为$F(vn)$。其次，算法需要从训练集中选择距离最小的$u$个训练样本。这是经典的最优搜索问题，最优FPTC为$F(nv+\ n{log}2u)$。因此，$k$NN分类器的总FPTC为$F(nv+n{log}_2u)$。考虑到相应的系数${\omega}{knn}$，$k$NN分类器的FPTC与实际运行时间$t’_{kNN}$关联如下：

\[t'_{kNN}=\omega_{kNN} \times t^*_{kNN} = \omega_{kNN} \times F(nv+nlog_2u)\]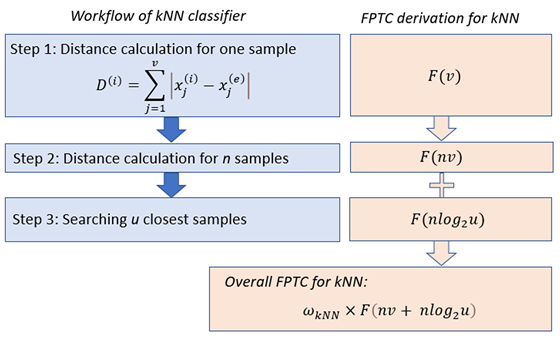

KNN分类器的FPTC推导过程示意图。

LR的FPTC推导

多分类LR分类器将其后验概率由Sigmoid变换替换为Softmax变换来执行多分类任务的。LR通常将L2范数作为正则化项加入到损失函数中，以提高LR分类器的稳定性和鲁棒性。根据我们的推导，具有L2范数和Softmax后验概率的LR的损失函数采用以下形式：

\[J(\boldsymbol{\theta}) = -\frac{1}{n} \cdot\sum_{i=1}^n\sum^m_{j=1}1\left\{y^{(i)}=j\right\}\cdot log\frac{exp(\boldsymbol{\theta}^T_j \textbf{x}^{(i)})}{\sum^m_{l=1}exp(\boldsymbol{\theta}^T_l\textbf{x}^{(i)})}+\frac{a}{2}\cdot\parallel\boldsymbol{\theta}\parallel^2_2\]

其中，$\boldsymbol{\theta }$是 $v\times m$ 的矩阵, $\boldsymbol{\theta }$ 中的元素是LR中的参数, ${\theta }_{pj}$ 是要素图层$p$中$j$类别的权重，$\alpha$的大小影响正则化强度。

LR分类器的目标是最小化损失函数时得到$\boldsymbol{\theta}$的最优值。随机平均梯度(stochastic average gradient, SAG) 是优化LR分类器的常用策略。SAG算法是对随机梯度下降算法(stochastic gradient descent，SGD)的一种改进。根据我们的推导，具有L2范数和Softmax变换的LR分类器中的参数 \(\boldsymbol{\theta}_j^T = \left\{\theta_{1j},\theta_{2j},\theta_{3j},......,\theta_{vj}\right\}\) 是根据公式5-7进行更新。

\[\boldsymbol{\theta}^{r+1}_j= \boldsymbol{\theta}^{r}_{j} -\frac{\lambda}{n} \sum^n_{i=1}z^r_i\] \[\textbf{z}^r_i= \begin{cases} \nabla_{\boldsymbol{\theta_{j}}}J(\boldsymbol{\theta})& if \ i=i_r\\ z_i^r & otherwise \end{cases}\] \[\nabla_{\boldsymbol{\theta_{j}}} J(\boldsymbol{\theta})= \textbf{x}^{(i)}(1\left\{y^{(i)}=j\right\})- \frac{exp(\boldsymbol{\theta}^T_j \textbf{x}^{(i)})}{\sum^m_{l=1}exp(\boldsymbol{\theta}^T_l\textbf{x}^{(i)})} +\alpha\boldsymbol{\theta}_j\]

其中， $\lambda$ 是学习率，$i_r\ $ 是从${1,\ 2,\ 3,\dots ,\ n}$ 中随机选出的第 $r$次迭代.

对于每次迭代，(公式5)-(公式7)便更新一次。因此，损失函数便根据(公式7)计算了一次。同时，具有$v$元素的$\boldsymbol{\theta_j}$便根据(公式6)更新了一次。基于上述分析，每次迭代的FPTC为$F(mvn)$。在多分类的LR中，假设对每个类别进行$q$次迭代后收敛（$q$为SAG过程中迭代次数），则总FPTC为$F(Qmvn)$。在这种情况下，$m$类别的FPTC为写为$F(Qm^2vn)$。最后，LR的FPTC与实际运行时间$t’_{LR}$关联如下，推导LR的FPTC的关键步骤如图所示：

\[t'_{LR}=\omega_{LR} \times t^*_{LR}=\omega_{LR}\times F(Qm^2vn)\]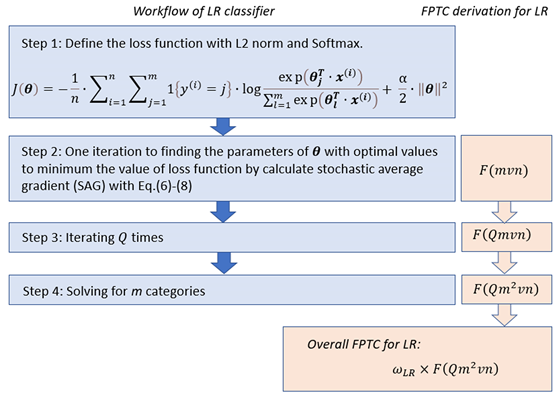

LR多分类器的FPTC推导过程示意图。

FPTC的验证与精度评价

为了验证FPTC的准确性，我们采用了三种评估方法：1)、用1：1的曲线图将实际运行时间与FPTC进行比较；2)、利用FPTC估计运行时间，并计算估计运行时间与观测运行时间之间的均方根误差(Root Mean Squared Error, RMSE)；3)、比较FPTC和TTC在不同特征选择下的实际运行时间。

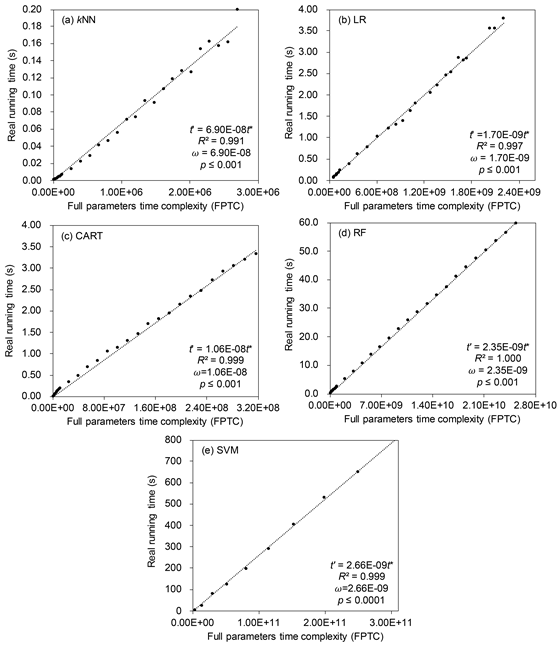
我们从训练数据集中随机选择子训练样本，并构造子训练样本集。对这些样本进行分类，并记录真实的运行时间。如图所示，FPTC与实际运行时间之间的线性关系表明了FPTC的有效性。5个分类器的R平方值均大于0.99($k$NN：0.991，LR：0.997，CART：0.999，RF：1.000，SVM：0.999)，表明FPTC的算法部分与实际运行时间之间存在极强的线性关系({p} $<$ 0.001)。

每一个算法的参数 $\omega$ 可以从各自相关性曲线的斜率中获得。

无论训练数据的大小如何，都可以基于两个可用的数据集粗略地估计斜率。这意味着可以通过在总数据集的两个小部分下预先运行算法来获得此值。由于系数$\omega$表示FPTC的物理部分，因此仅当算法应用于不同的计算环境时，该值才会改变。

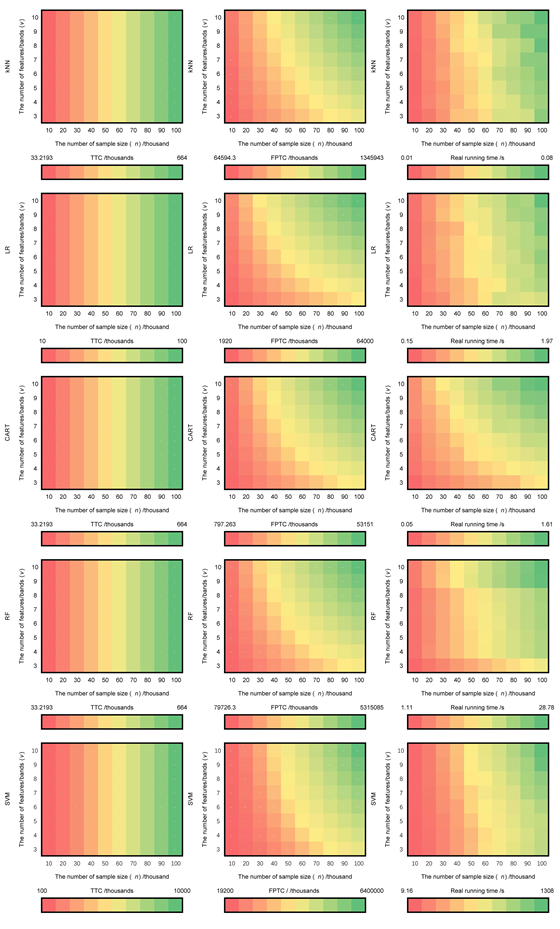
TTC(左列)和FPTC(中列)与实际运行时间(右列)的比较。

此外，FPTC还可以通过不同的参数反映运行时间的变化。当n个训练样本由低到高变化，且其他影响参数保持不变时，支持向量机的FPTC最容易受到这种变化的影响，其次是RF、CART、kNN和LR。如果n从1变为128，则LR的FPTC增加128倍，kNN增加128倍多，CART和RF增加896倍，SVM增加16,384倍以上。当分类数m由低变高且其他影响参数保持不变时，支持向量机和LR的FPTC最容易受到这种变化的影响，其次是CART和RF，而kNN则不受影响。例如，如果m从两个类变为200个类，则SVM和LR的FPTC增加10,000倍，CART和RF的FPTC增加100倍。当特征数或波段数v由低变高且其他影响参数不变时，SVM、LR、CART和RF的时间复杂度在多项式时间内变化，而kNN的时间复杂度受影响较小。
其次，为了进一步说明FPTC和TTC的差异，我们分析了在不同波段(v=3, 4, 5,…,10)和不同样本大小(n=10, 20, 30,…,100,000)的所有组合下，FPTC和TTC的变化趋势，并与实际运行时间趋势进行了比较。在图9中，TTC、FPTC和实际运行时间的值以红色到绿色从低到高映射。结果表明，TTC对v的变化没有反应，而FPTC能更好地反映v的变化。
正如我们所看到的，在不同的带宽和数据大小下，FPTC显示出与实际运行时间相似的模式。TTC的模式是不同的，因为TTC忽略了不同特征/波段的影响。

总结

在自然灾害应急响应中，准确的时间预测有助于应急管理者在有限的时间和资源下选择分类算法。在本研究中，我们提出了FPTC和系数$\omega$来估计每个分类器的运行时间。通过研究分类器程序的总体结构及其数学原理，推导出五种常见分类器($k$NN、LR、CART、RF和SVM)的FPTC。根据实际运行时间与FPTC之间的关系，建立了线性回归模型，并由线性回归得到了系数$\omega $。然后，我们准确地预测了每个分类器的运行时间，并筛选出合适的分类器。研究结果可概括如下：

• 提出了一种定量评估机器学习分类器时间效率的方法–FPTC。我们推导了五种通用分类器的FPTC。结果表明$k$NN 的FPTC 是 $F(nv+\ n{log}_2u)$, LR的FPTC是 $F(Qm^2vn)$, CART的FPTC是 $F((m+1)nv{log}_2n)$), RF是FPTC是 $F(s(m+1)nv{log}_2n)$, SVM的FPTC是 $F(m^2Qv\ (n+k))$.

• 在我们的研究中，FPTC与运行时间之间存在很强的线性关系 (${R}^2$ $\geq 0.991$, $\ p\le 0.001$)。 这种线性关系验证了FPTC推导过程的正确性。每种算法的修正系数都可以从强线性回归中得到。

• 每个分类器的运行时间用FPTC中的系数$\omega$来估计。研究表明，实际运行时间与估计运行时间之间的平均均方根误差为3.34s，说明了用FPTC预测算法运行时间的可行性和准确性。

• 研究表明，支持向量机的训练参数$Q$与样本数有显著的线性相关关系($R^2=1.00$), 而LR的$Q$是稳定的，不随$n$的变化而变化。根据上述规则，支持向量机的总FPTC被修正为$F(m^2vn^2)$，LR的总FPTC被修正为$F(m^2vn)$。更新的FPTC不受程序是否提前运行的影响。

未来的研究中，我们计划为算法推导出更多的FPTC值。对于紧急任务，可以快速筛选出精度高、FPTC低的合适算法，帮助应急管理人员根据可获得的遥感数据量，快速做出应对自然灾害的决策。