$$ \newcommand{\bone}{\mathbf{1}} \newcommand{\bbeta}{\mathbf{\beta}} \newcommand{\bdelta}{\mathbf{\delta}} \newcommand{\bepsilon}{\mathbf{\epsilon}} \newcommand{\blambda}{\mathbf{\lambda}} \newcommand{\bomega}{\mathbf{\omega}} \newcommand{\bpi}{\mathbf{\pi}} \newcommand{\bphi}{\mathbf{\phi}} \newcommand{\bvphi}{\mathbf{\varphi}} \newcommand{\bpsi}{\mathbf{\psi}} \newcommand{\bsigma}{\mathbf{\sigma}} \newcommand{\btheta}{\mathbf{\theta}} \newcommand{\btau}{\mathbf{\tau}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bb}{\mathbf{b}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\boldf}{\mathbf{f}} \newcommand{\bg}{\mathbf{g}} \newcommand{\bh}{\mathbf{h}} \newcommand{\bi}{\mathbf{i}} \newcommand{\bj}{\mathbf{j}} \newcommand{\bk}{\mathbf{k}} \newcommand{\bell}{\mathbf{\ell}} \newcommand{\bm}{\mathbf{m}} \newcommand{\bn}{\mathbf{n}} \newcommand{\bo}{\mathbf{o}} \newcommand{\bp}{\mathbf{p}} \newcommand{\bq}{\mathbf{q}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bt}{\mathbf{t}} \newcommand{\bu}{\mathbf{u}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\bA}{\mathbf{A}} \newcommand{\bB}{\mathbf{B}} \newcommand{\bC}{\mathbf{C}} \newcommand{\bD}{\mathbf{D}} \newcommand{\bE}{\mathbf{E}} \newcommand{\bF}{\mathbf{F}} \newcommand{\bG}{\mathbf{G}} \newcommand{\bH}{\mathbf{H}} \newcommand{\bI}{\mathbf{I}} \newcommand{\bJ}{\mathbf{J}} \newcommand{\bK}{\mathbf{K}} \newcommand{\bL}{\mathbf{L}} \newcommand{\bM}{\mathbf{M}} \newcommand{\bN}{\mathbf{N}} \newcommand{\bP}{\mathbf{P}} \newcommand{\bQ}{\mathbf{Q}} \newcommand{\bR}{\mathbf{R}} \newcommand{\bS}{\mathbf{S}} \newcommand{\bT}{\mathbf{T}} \newcommand{\bU}{\mathbf{U}} \newcommand{\bV}{\mathbf{V}} \newcommand{\bW}{\mathbf{W}} \newcommand{\bX}{\mathbf{X}} \newcommand{\bY}{\mathbf{Y}} \newcommand{\bZ}{\mathbf{Z}} \newcommand{\bsa}{\boldsymbol{a}} \newcommand{\bsb}{\boldsymbol{b}} \newcommand{\bsc}{\boldsymbol{c}} \newcommand{\bsd}{\boldsymbol{d}} \newcommand{\bse}{\boldsymbol{e}} \newcommand{\bsoldf}{\boldsymbol{f}} \newcommand{\bsg}{\boldsymbol{g}} \newcommand{\bsh}{\boldsymbol{h}} \newcommand{\bsi}{\boldsymbol{i}} \newcommand{\bsj}{\boldsymbol{j}} \newcommand{\bsk}{\boldsymbol{k}} \newcommand{\bsell}{\boldsymbol{\ell}} \newcommand{\bsm}{\boldsymbol{m}} \newcommand{\bsn}{\boldsymbol{n}} \newcommand{\bso}{\boldsymbol{o}} \newcommand{\bsp}{\boldsymbol{p}} \newcommand{\bsq}{\boldsymbol{q}} \newcommand{\bsr}{\boldsymbol{r}} \newcommand{\bss}{\boldsymbol{s}} \newcommand{\bst}{\boldsymbol{t}} \newcommand{\bsu}{\boldsymbol{u}} \newcommand{\bsv}{\boldsymbol{v}} \newcommand{\bsw}{\boldsymbol{w}} \newcommand{\bsx}{\boldsymbol{x}} \newcommand{\bsy}{\boldsymbol{y}} \newcommand{\bsz}{\boldsymbol{z}} \newcommand{\bsA}{\boldsymbol{A}} \newcommand{\bsB}{\boldsymbol{B}} \newcommand{\bsC}{\boldsymbol{C}} \newcommand{\bsD}{\boldsymbol{D}} \newcommand{\bsE}{\boldsymbol{E}} \newcommand{\bsF}{\boldsymbol{F}} \newcommand{\bsG}{\boldsymbol{G}} \newcommand{\bsH}{\boldsymbol{H}} \newcommand{\bsI}{\boldsymbol{I}} \newcommand{\bsJ}{\boldsymbol{J}} \newcommand{\bsK}{\boldsymbol{K}} \newcommand{\bsL}{\boldsymbol{L}} \newcommand{\bsM}{\boldsymbol{M}} \newcommand{\bsN}{\boldsymbol{N}} \newcommand{\bsP}{\boldsymbol{P}} \newcommand{\bsQ}{\boldsymbol{Q}} \newcommand{\bsR}{\boldsymbol{R}} \newcommand{\bsS}{\boldsymbol{S}} \newcommand{\bsT}{\boldsymbol{T}} \newcommand{\bsU}{\boldsymbol{U}} \newcommand{\bsV}{\boldsymbol{V}} \newcommand{\bsW}{\boldsymbol{W}} \newcommand{\bsX}{\boldsymbol{X}} \newcommand{\bsY}{\boldsymbol{Y}} \newcommand{\bsZ}{\boldsymbol{Z}} \newcommand{\calA}{\mathcal{A}} \newcommand{\calB}{\mathcal{B}} \newcommand{\calC}{\mathcal{C}} \newcommand{\calD}{\mathcal{D}} \newcommand{\calE}{\mathcal{E}} \newcommand{\calF}{\mathcal{F}} \newcommand{\calG}{\mathcal{G}} \newcommand{\calH}{\mathcal{H}} \newcommand{\calI}{\mathcal{I}} \newcommand{\calJ}{\mathcal{J}} \newcommand{\calK}{\mathcal{K}} \newcommand{\calL}{\mathcal{L}} \newcommand{\calM}{\mathcal{M}} \newcommand{\calN}{\mathcal{N}} \newcommand{\calO}{\mathcal{O}} \newcommand{\calP}{\mathcal{P}} \newcommand{\calQ}{\mathcal{Q}} \newcommand{\calR}{\mathcal{R}} \newcommand{\calS}{\mathcal{S}} \newcommand{\calT}{\mathcal{T}} \newcommand{\calU}{\mathcal{U}} \newcommand{\calV}{\mathcal{V}} \newcommand{\calW}{\mathcal{W}} \newcommand{\calX}{\mathcal{X}} \newcommand{\calY}{\mathcal{Y}} \newcommand{\calZ}{\mathcal{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\F}{\mathbb{F}} \newcommand{\Q}{\mathbb{Q}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \newcommand{\nnz}[1]{\mbox{nnz}(#1)} \newcommand{\dotprod}[2]{\langle #1, #2 \rangle} \newcommand{\ignore}[1]{} \let\Pr\relax \DeclareMathOperator*{\Pr}{\mathbf{Pr}} \newcommand{\E}{\mathbb{E}} \DeclareMathOperator*{\Ex}{\mathbf{E}} \DeclareMathOperator*{\Var}{\mathbf{Var}} \DeclareMathOperator*{\Cov}{\mathbf{Cov}} \DeclareMathOperator*{\stddev}{\mathbf{stddev}} \DeclareMathOperator*{\avg}{avg} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\dist}{dist} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\spn}{span} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\codim}{codim} \DeclareMathOperator{\diag}{diag} \newcommand{\PTIME}{\mathsf{P}} \newcommand{\LOGSPACE}{\mathsf{L}} \newcommand{\ZPP}{\mathsf{ZPP}} \newcommand{\RP}{\mathsf{RP}} \newcommand{\BPP}{\mathsf{BPP}} \newcommand{\P}{\mathsf{P}} \newcommand{\NP}{\mathsf{NP}} \newcommand{\TC}{\mathsf{TC}} \newcommand{\AC}{\mathsf{AC}} \newcommand{\SC}{\mathsf{SC}} \newcommand{\SZK}{\mathsf{SZK}} \newcommand{\AM}{\mathsf{AM}} \newcommand{\IP}{\mathsf{IP}} \newcommand{\PSPACE}{\mathsf{PSPACE}} \newcommand{\EXP}{\mathsf{EXP}} \newcommand{\MIP}{\mathsf{MIP}} \newcommand{\NEXP}{\mathsf{NEXP}} \newcommand{\BQP}{\mathsf{BQP}} \newcommand{\distP}{\mathsf{dist\textbf{P}}} \newcommand{\distNP}{\mathsf{dist\textbf{NP}}} \newcommand{\eps}{\epsilon} \newcommand{\lam}{\lambda} \newcommand{\dleta}{\delta} \newcommand{\simga}{\sigma} \newcommand{\vphi}{\varphi} \newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\wt}[1]{\widetilde{#1}} \newcommand{\wh}[1]{\widehat{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\ot}{\otimes} \newcommand{\zo}{\{0,1\}} \newcommand{\co}{:} %\newcommand{\co}{\colon} \newcommand{\bdry}{\partial} \newcommand{\grad}{\nabla} \newcommand{\transp}{^\intercal} \newcommand{\inv}{^{-1}} \newcommand{\symmdiff}{\triangle} \newcommand{\symdiff}{\symmdiff} \newcommand{\half}{\tfrac{1}{2}} \newcommand{\mathbbm}{\Bbb} \newcommand{\bbone}{\mathbbm 1} \newcommand{\Id}{\bbone} \newcommand{\SAT}{\mathsf{SAT}} \newcommand{\bcalG}{\boldsymbol{\calG}} \newcommand{\calbG}{\bcalG} \newcommand{\bcalX}{\boldsymbol{\calX}} \newcommand{\calbX}{\bcalX} \newcommand{\bcalY}{\boldsymbol{\calY}} \newcommand{\calbY}{\bcalY} \newcommand{\bcalZ}{\boldsymbol{\calZ}} \newcommand{\calbZ}{\bcalZ} $$

基于HRU-Net的中高分辨率地表要素提取模型

Created in March 08, 2023 by Shanxin Guo

2023   ·   machine-learning   remote-sensing

post.cover
大理洱海

研究背景

耕地作为重要的土地利用/覆盖类型，其数量、质量和空间分布直接关系到人类社会经济发展和国家粮食安全，同时也与生态环境保护密切相关。准确、快速地获取耕地信息是土地利用/覆盖研究领域的热点之一。

遥感技术为耕地信息提取提供了高效、全面、准确的手段，通过遥感图像分类方法获取耕地分布、类型及面积等信息，对于优化作物种植结构和管理具有重要意义。

传统遥感分类方法（如 SVM、KNN 和 RF）在耕地提取中面临以下三大难点：

  1. 同物异谱现象严重
    耕地上种植的作物类型多样，灌溉方式和土壤类型存在差异，同时休耕期的耕地光谱特征差异显著，传统方法难以适应。

  2. 特征泛化能力不足
    传统方法依赖有限的特征，这些特征往往针对具体问题设计，跨地域应用时表现不佳。

  3. 算法复杂度高
    基于统计学习的传统算法在处理大规模遥感数据时，易出现训练困难或精度饱和的问题。

近年来，深度学习在遥感图像分类领域发展迅速，主要分为图片级分类和像素级分类两种方法：

  • 图片级分类方法
    以整幅图像为判别单元，适用于地物识别和提取场景。

  • 像素级分类方法
    以每个像素为判别单元，采用全卷积网络（FCN）实现端到端的分类，保留了图像的空间信息，显著提高了分类效率。

然而，在像素级分类中，为提取多尺度特征，深度卷积网络通常将高分辨率图像降采样为低分辨率图像，这一过程导致高分辨率信息（如边缘、梯度等）的丢失，影响分类精度和细节表现。

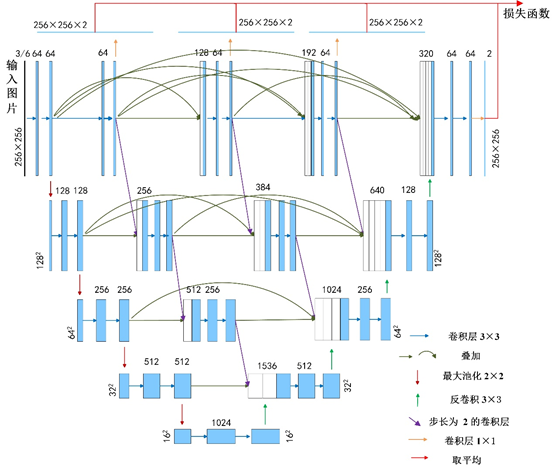
高分辨率 U-Net（HRU-Net）算法介绍

本文提出的 HRU-Net 方法在保留 U-Net 网络对称结构的基础上，进行了以下两点改进：

  1. 改进跳跃连接结构
    采用高分辨率信息保留思想，优化 U-Net 的跳跃连接。

  2. 引入深度监督机制
    在损失函数中加入深度监督，进一步利用高分辨率信息优化网络参数。

HRU-Net 网络结构示意图

HRU-Net 与 U-Net、U-Net++ 和 RF 的比较

实验从以下三个方面对 HRU-Net、U-Net、U-Net++ 和 RF 进行了比较：

  1. 总体精度
  2. 边缘细节准确性
  3. 类间变化鲁棒性

结果表明，HRU-Net 在所有指标上均优于其他方法，尤其在包含 NIR 和 SWIR 波段的 TM-All 数据集上表现最佳。

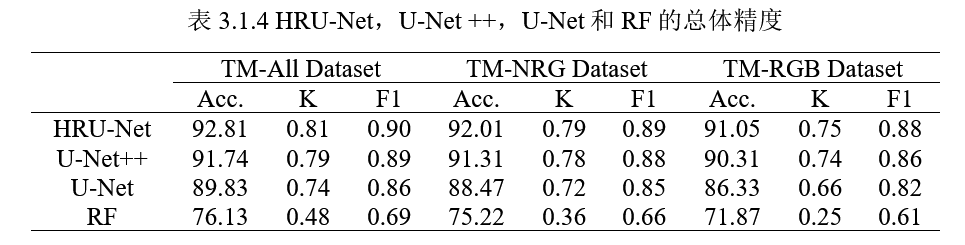
表 3.1.4 显示了不同方法在测试数据集上的精度评估。HRU-Net 在总体精度、Kappa 系数和 F1-score 上均取得最高值，特别是在 TM-All 数据集上，总体精度达到 92.81%，显著优于其他方法。

不同模型在测试数据集上的精度评估

边缘细节的准确性

如图 3.1.8 所示，通过目视解译评估边缘细节的准确性。HRU-Net 的结果边缘更清晰，细节更丰富，与 U-Net++ 和 U-Net 相比，保留了更多的边界信息，而 RF 的结果边缘模糊，无法正确检测类间变化。

HRU-Net、U-Net 和随机森林模型在三个数据集的输出图对比

结论

本文提出的 HRU-Net 网络针对以下两大问题进行了改进：

  1. 同物异谱问题
    传统方法难以提取休耕期耕地，HRU-Net 通过改进跳跃连接结构解决了这一问题。

  2. 高分辨率信息丢失问题
    HRU-Net 通过全程保留高分辨率信息和引入深度监督机制，显著提高了分类精度和细节表现。

实验结果表明，HRU-Net 在耕地提取精度、边缘细节和类间变化鲁棒性方面均优于 U-Net、U-Net++ 和 RF，验证了其在遥感地物分类中的有效性。

原文链接

Xu, W., Deng, X., Guo, S., Chen, J., Sun, L., Zheng, X., Xiong, Y., Shen, Y., & Wang, X. (2020). High-Resolution U-Net: Preserving Image Details for Extraction Cultivated Land. Sensors, 20(15), 4064.
https://www.mdpi.com/1424-8220/20/15/4064/html



    Enjoy Reading This Article?

    Here are some more articles you might like to read next:

  • 基于时空融合的MODIS产品降尺度模型-以海表叶绿素为例
  • 面向地表快速变化场景的时空融合的动态神经网络I-USTFM：以地表温度为例
  • 对抗样本噪声的遥感深度学习分类网络模型
  • 快速评估监督学习中常用遥感分类算法的时间效率
  • 基于光学微波特征融合的典型经济作物提取