面向地表快速变化场景的时空融合的动态神经网络I-USTFM：以地表温度为例

原文链接

Guo, S., Li, M., Li, Y., Chen, J., Zhang, H. K., Sun, L., Wang, J., Wang, R., & Yang, Y. (2024). The Improved U-STFM : A Deep Learning-Based Nonlinear Spatial-Temporal Fusion Model for Land Surface Temperature Downscaling. Remote Sensing, 16(322), 1–28.

研究背景

卫星热传感器提供的陆地表面温度（LST）数据能够详细捕捉地球表面能量分布在空间和时间上的变化。这些数据在蒸散观测和城市热建模等领域具有重要应用[1-3]。然而，由于卫星轨道和传感器设计的限制，热波段的空间分辨率和时间分辨率之间存在权衡。日常传感器如 MODIS LST 的分辨率为 1 公里，而精细分辨率（100 米或更低）的传感器如 Landsat 系列卫星，受限于扫描带宽和轨道高度，仅能提供数天内的数据。因此，如何整合多个卫星传感器的数据以获得高时空分辨率的观测数据，成为提升卫星资源利用率的关键挑战之一。这一挑战的解决将进一步推动地表能量建模和精准农业等综合应用的发展[3]。

为克服这一限制，近年来在计算机视觉和遥感领域开发了许多超分辨率或融合模型，用于生成具有精细空间分辨率的每日 LST 数据。这些模型主要分为三类：(1) 基于学习的；(2) 基于回归的；(3) 基于时空融合的。

基于学习的模型

基于学习的模型假设粗像素和细像素之间的关系可以用点扩散函数（PSF）来描述。PSF 表示低分辨率像素与高分辨率像素的混合过程，具有时空一致性，可通过学习建模。早期的 PSF 模型主要基于图像重建方法，如核方法[5]、解卷积模型[6]、稀疏编码[7-9] 和基于 SVM 的方法[10]。随着深度学习技术的进步，SRCNN[11] 和 SRGAN[12] 等深度网络被引入超分辨率问题，并进一步应用于遥感领域，如 STFDCNN[13]、GAN-STFM[21] 等模型。这类模型的优势在于训练后预测准确且高效。然而，由于 LST 的快速变化，通用 PSF 难以捕捉低分辨率图像的混合特性。此外，基于深度学习的模型缺乏物理原理指导，难以解释不可靠预测的原因。

基于回归的模型

基于回归的模型假设热波段值可以通过辅助生物物理参数（如地表反射率、植被指数等）建模。早期模型如 DisTrad[23] 和 TsHARP[24] 利用植被指数与 LST 的关系进行降尺度。近年来，随机森林回归[26] 和高斯滤波法[22] 等非线性方法被用于改进模型性能。然而，这类模型假设 LST 与预测因子的关系在空间上不变，可能不适用于区域尺度。此外，模型性能依赖于辅助数据的分辨率和准确性。

基于时空融合的模型

基于时空融合的模型利用地表动态的时空连续性特征，通过时间序列数据捕捉粗像素和细像素的关系。这类模型无需考虑缩减比例问题，适用于捕捉物候和土地覆被变化。典型模型包括 STARFM[33]、ESTARFM[36] 和 U-STFM[41] 等。然而，这些模型在处理 LST 快速变化和抗噪声能力方面仍存在挑战。

I-USTFM 模型的改进

针对当前时空融合模型的局限性，本研究提出了一种改进的 U-STFM 模型（I-USTFM），结合了深度学习组件 DyNet 和 RatioNet，用于非线性解混和抗噪加权。I-USTFM 的主要目标如下：

开发 DyNet，用于非线性解混。
利用 RatioNet 提高加权函数的抗噪能力。
扩展 U-STFM 模型以适应高时间变异性的传感器，生成 30 米分辨率的每日 LST 产品。

数据源及研究区

研究区域

随着城市化的快速发展，城市热岛效应对城市及周边地区的生态环境产生了重大影响。城市热岛效应是指城市温度高于周边农村地区的现象。造成这种温差的主要原因是人类活动和城市基础设施，如建筑物、人行道和交通系统，它们比自然景观更有效地吸收和保留热量。随着城市继续快速发展和城市化，城市热岛效应变得更加明显。这种现象会导致各种环境和生态后果。例如，它会影响当地气候、空气质量、能源消耗，甚至人类健康。因此，了解和缓解城市热岛效应对于创建可持续发展的宜居城市至关重要，而这在很大程度上依赖于高时空分辨率的地表温度监测数据。

粤港澳大湾区（GBA）是中国正在经历快速城市化的地区。在粤港澳大湾区内，东莞市和深圳市作为主要的城市中心，随着国家经济的快速发展，在土地利用和城市发展方面发生了重大变化。大面积的荒地和林地被改造成城市区域，导致地表温度空间模式的快速变化。

本研究选择了粤港澳大湾区的一部分作为研究区域，面积约为 1843 平方公里（介于东经 113°49′13″- 114°16′10″ 和北纬 22°37′17″-22°59′48″之间），如图 1所示。所选区域地形复杂，土地覆被类型多样，为评估时空融合模型（STFM）处理土地覆被快速变化的能力提供了一个综合场景。

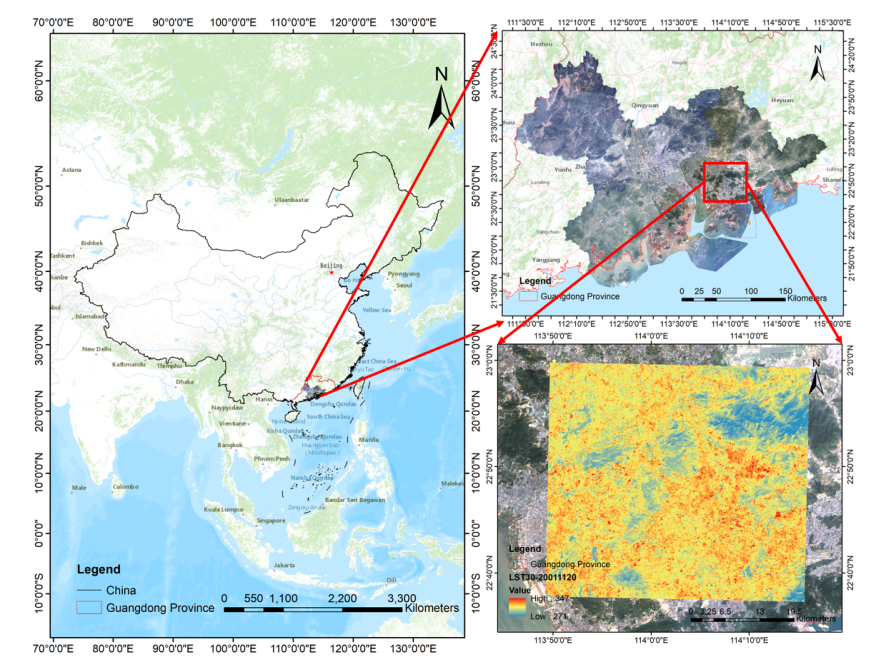
图1研究区域

数据集

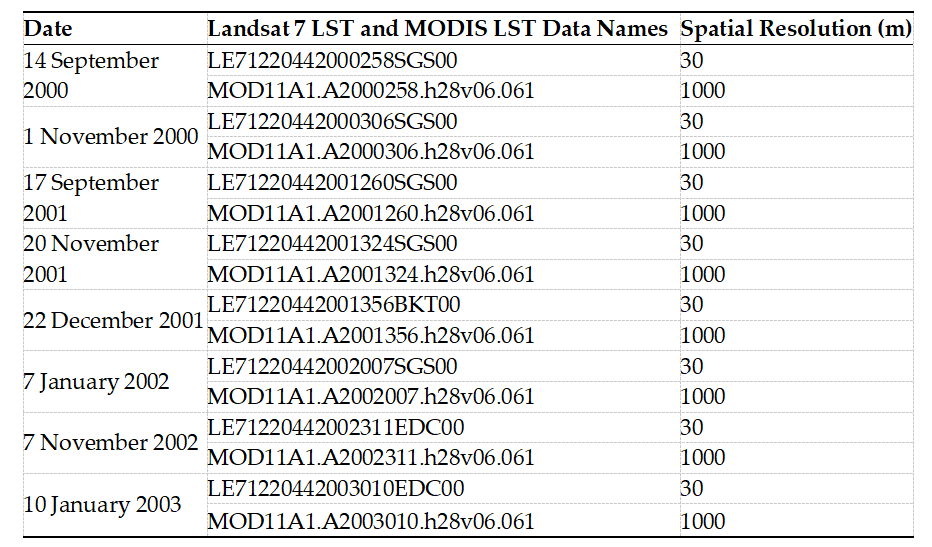
与Landsat 7 号的地表温度产品相比，MODIS Terra的日间地表温度产品被用于从 1000 米降到 30 米。在本研究中，两颗卫星在同一日期的地表温度（LST）的微小差异被视为系统误差，可以忽略不同日期之间巨大的地表温度差异。MODIS LST产品（MOD11A1.006）和Landsat7 ETM + LST 产品（Landsat 7 ETM Plus Collection 2 Level-2）来自USGS Earth Explorer（https://earthexplorer.usgs.gov（2022 年 4 月 12 日访问））。经USGS处理后，ETM + LST 的空间分辨率为30米，重访频率为16天。由于ETM + SLC在2003年5月31日后失效，加上研究区域常年阴雨，本研究选择了2000年9月至2003 年5月期间云量阈值小于1%的数据，收集了8对有效的Landsat7 LST和MODIS LST图像。详情见表 1。

表1研究区域使用的Landsat 7 LST 和 MODIS LST 产品列表

模型方法介绍

原始U-STFM

在本研究中，我们选择U-STFM作为基线模型。U-STFM模型最早是由Huang和Zhang于 2014 年针对地表反射率数据提出的。该模型是一种典型的基于解混的STFM模型，包含线性解混函数和加权函数。关于U-STFM的详细解释可参见原论文[41]。我们在此对U-STFM进行简要介绍。

原始 U-STFM 的问题

在本研究中，我们主要关注与原始 U-STFM 相关的两个关键问题。第一个问题与原始解混函数的线性不稳定性有关，第二个问题与原始加权函数的误差敏感性有关。

解混函数在时空数据融合模型中起着至关重要的作用。最初的解混函数基于线性解混理论，该理论假定粗像素的能量可表示为精细分辨率像素的线性组合，并按其覆盖率分数加权。如图 1 所示，通过线性解混函数，我们可以在 MODIS 层面上分配多个变化率，并利用覆盖分数矩阵来确定 HCR 层面上的时间变化率。当图像数量超过未知值数量时，该函数就可以求解。通常情况下，由于本研究区域的 MODIS 像素数量明显多于 HCR 数量，因此可以满足这一条件。但是，如图 2所示，当 HCR 数量增加时，覆盖率矩阵（红色突出显示）变得稀疏，导致线性系统的不稳定性增加。

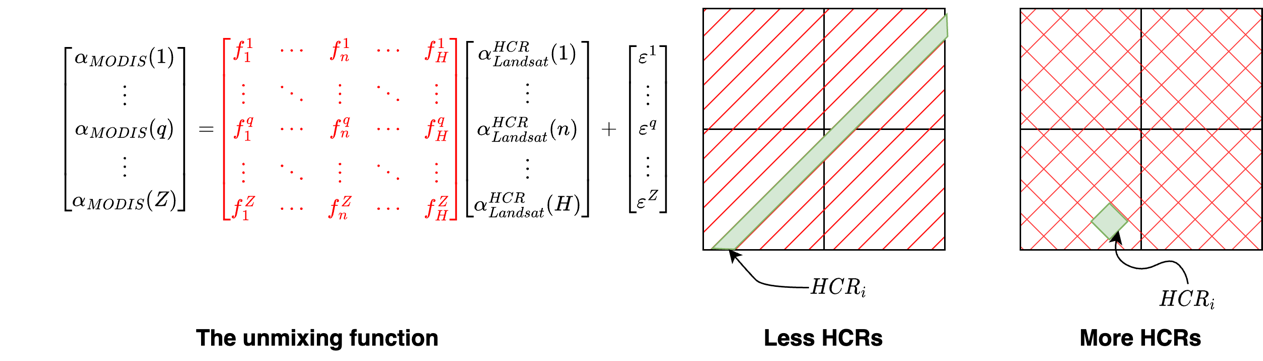
图 2解混函数的局限性。红色区域代表HCR，黑色方块代表MODIS像素。左图中的绿色区域表示HCR跨多个MODIS像素的情况，右图中的绿色区域表示HCR只被一个MODIS像素覆盖的情况，这是使覆盖派系矩阵更加稀疏的结果。

通过将目标日期之前和之后的精细图像与HCR层面的 LST变化率合成，预测出精细分辨率图像。然而，如图 3所示，这种加权函数的问题在于，当包含误差时，LST预测误差会表现出不同的敏感度。更具体地说，在红色区域内，即使是微小的变化也会导致LST预测结果的巨大差异。该区域内的误差容限相对较小。

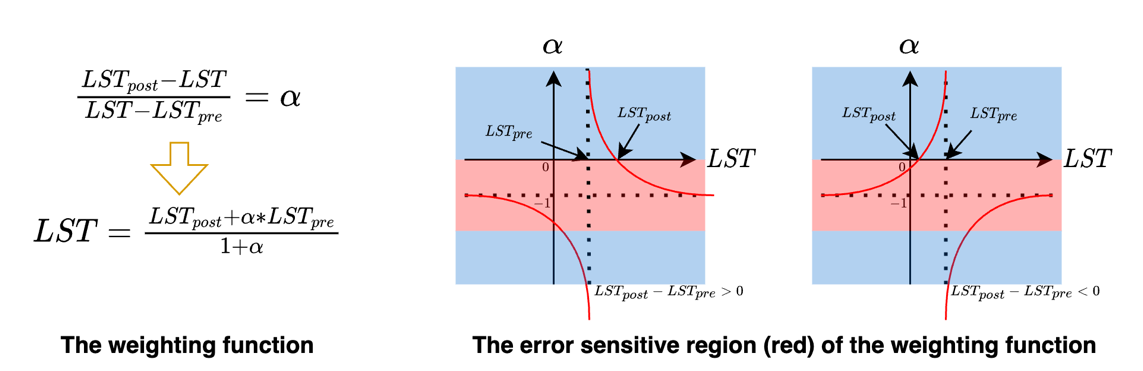
原始加权函数的问题：红色区域代表误差敏感度较高的区域；蓝色区域代表敏感度较低的区域。

I-USTFM

非线性U-STFM继承了U-STFM模型的尺度不变性，是一种基于解混的 STFM模型，假定MODIS和Landsat时间序列中的热信号变化比相同。因此，在尺度不变性假设下，MODIS时间序列中捕获的变化率可应用于Landsat序列。

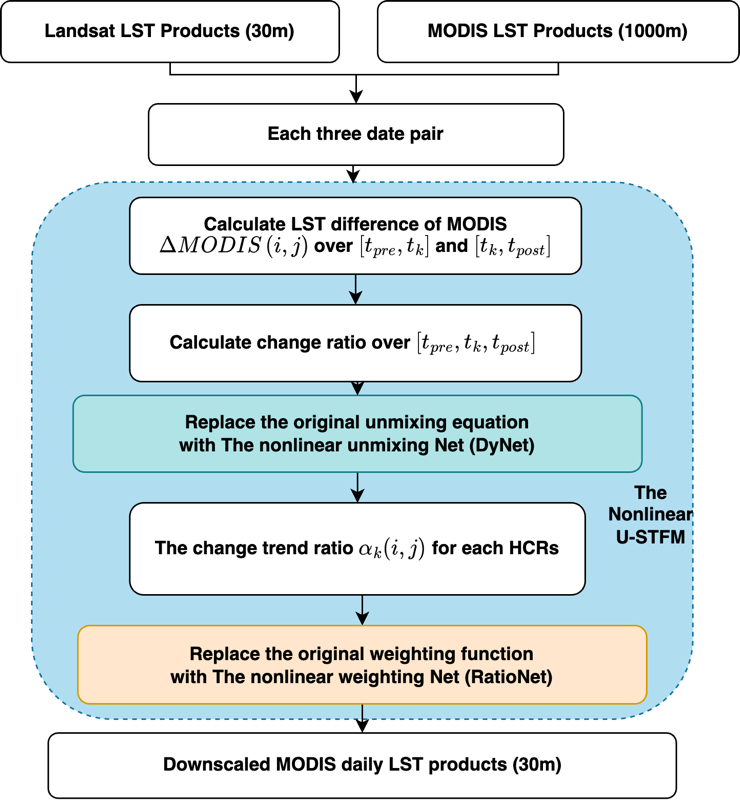
根据这一想法，我们设计了两个多层感知器（DyNet和RatioNet），在解混和加权过程中形成数据驱动的非线性预测。如图 4所示，预测目标日期的 30 米级陆地表面温度（LST）时，需要将前一日期，目标日期和后续日期的MODIS LST数据组织成三个日期对。随后，可以计算MODIS LST数据集中不同日期之间的LST差值。此外，还可以计算MODIS每个像素的变化率，并将其作为DyNet 模型的输入。DyNet的输出提供了每个HCR的变化率，这反过来又成为RatioNet的输入，从而获得目标日期LST的最终预测结果。

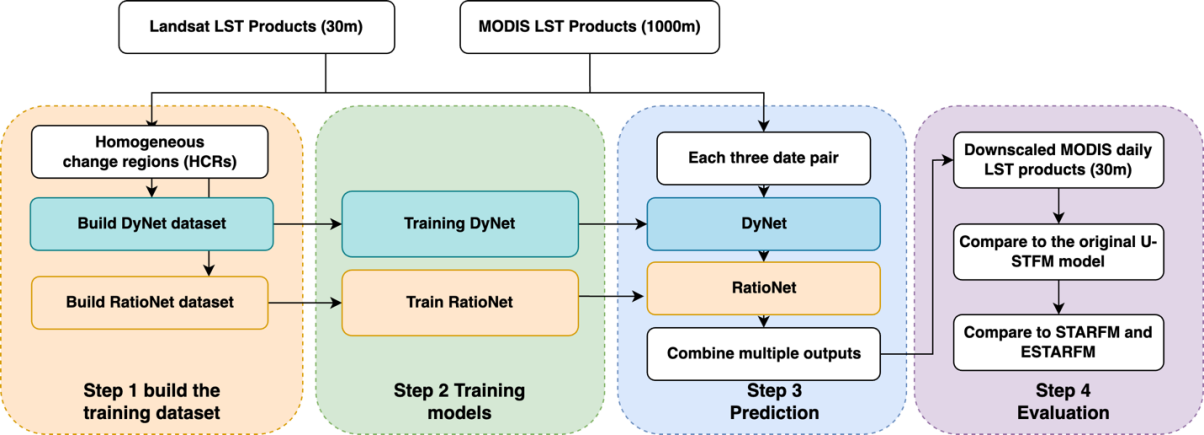
与最初的 U-STFM 不同，I-USTFM 是一种数据驱动模型，使用适当的数据集进行训练。本研究的工作流程如图 5所示。主要分为四个步骤。第 1 步：确定同质变化区域（HCR）。HCR被确定为具有相似LST变化趋势并可共享相似变化率的区域，以便进行下一步工作。利用时间序列高分辨率Landsat数据建立特征空间，以识别HCR，并建立用于训练的数据集。步骤2：训练DyNet 和 RatioNet。这一步的主要任务是训练模型，以捕捉MODIS与子像素HCR之间变化率的非线性关系。训练完成后，非线性U-STFM模型将用于预测基于时间序列MODIS和Landsat数据的更高分辨率LST产品。第四步，我们将非线性模型与原始U-STFM模型以及两种常用降尺度模型STARFM和ESTARFM进行了比较，评估了非线性模型的性能。

在统一的太阳辐射和蒸发条件下，相似的地表材料或土地覆被类型随着时间的推移呈现出相似的热模式。表现出相似变化规律的区域被确定为同质变化区域。每个同质变化区域都有相似的变化率，可作为解混过程的指标。在 U-STFM模型中，HCR是由分割过程定义的。考虑到模型的跨时间泛化，我们根据聚类方法定义了HCR。具体来说，我们使用k-means聚类法来定义用于预测的 HCR。本研究对不同数量的类进行了比较。

非线性解混模型（DyNet）

考虑到热信号的辐射效应，UTFM使用的传统线性解混模型并不合适，因为热点（HCR）可能会根据 MODIS信号的温度对其产生更大的影响。HCR与 MODIS信号之间的关系似乎是非线性的。

为了克服解混函数不稳定的问题，我们根据历史数据集引入了动态多层感知器（DyNet）来捕捉这种非线性关系。工作流程如图 6所示。

DyNet的训练数据集是利用Landsat和MODIS LST历史产品计算得出的。DyNet的输入是MODIS LS在三个日期的时间变化率，分别代表前一个日期、目标日期和后一个日期。DyNet 的输出是 HCR 水平的时间变化率，即 30 米水平的平均值。和的计算遵循公式 (2)。

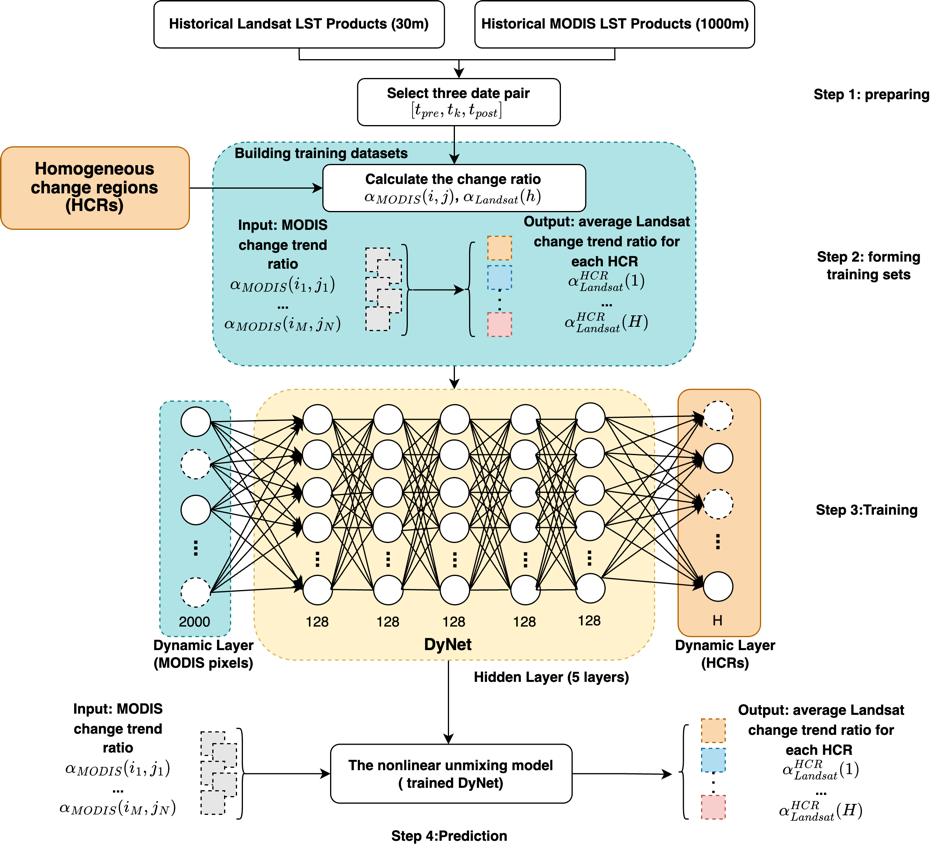
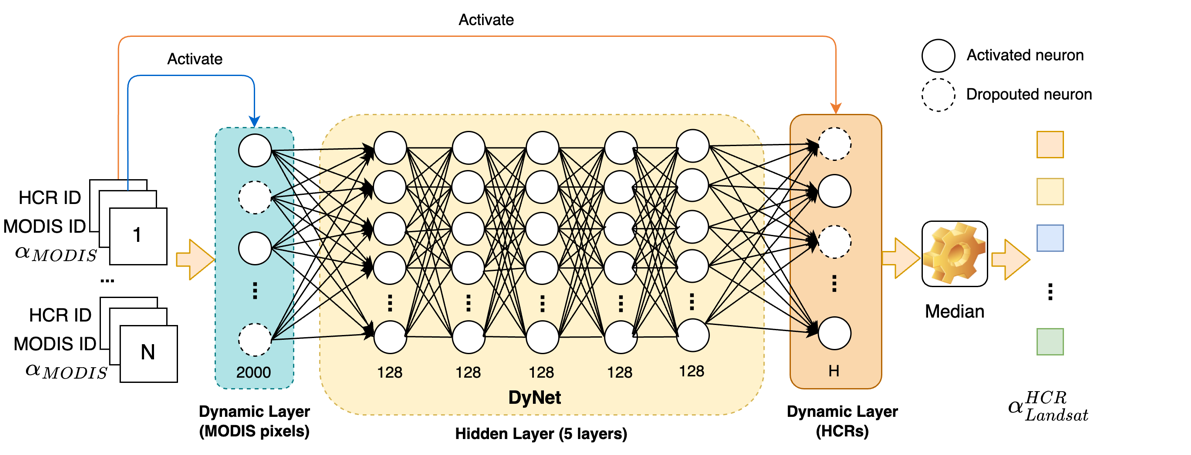
DyNet有两个动态层作为输入层和输出层，还有五个隐藏层，每层有 128 个神经元。所有七个层都是全连接的，以捕捉非线性关系。整个结构可解释为与一组 MODIS像素（本研究中为 2000 个）进行解混，其中，表示由聚类或分割算法定义的 HCR 数量。DyNet的训练过程基于小批量随机梯度下降法。如图 7所示，输入层中的神经元代表用于解决非线性解混问题的 MODIS 像素总数。例如，如果选择 2000 个MODIS像素进行解混，就会有 2000 个神经元。DyNet对输入层的数量没有具体要求，因为这些 MODIS 像素可以覆盖所有同质变化区域（HCR）。为避免潜在的 “姿态不佳问题”，建议使用足够多的 MODIS 像素，以确保覆盖所有HCR。这一数量可作为模型的超参数。我们根据该地区 4000 多个MODIS像素的总数，随机抽取了一半的MODIS像素（2000 个），以确保覆盖所有HCR。输出层中的神经元代表HCR的变化率。由于每个批次只包含特定的MODIS像素和HCR，因此输入层和输出层仅由该特定批次中的MODIS像素和HCR激活。不属于当前批次的神经元会被剔除。因此，输入和输出层在训练过程中会发生动态变化。由于每个批次都给出了部分预测值，因此最终预测值是通过使用每个HCR的中值计算将每个批次的多个预测值组合起来得到的。中值用于减轻离群预测的影响，因为它们对平均值的影响更大。均方误差 (MSE) 被用作训练时的损失函数。在将模型从一个区域应用到另一个区域时，如果各区域采用相同的聚类或分割规则，则模型可以重复使用，无需重新训练。

非线性加权模型（RatioNet）

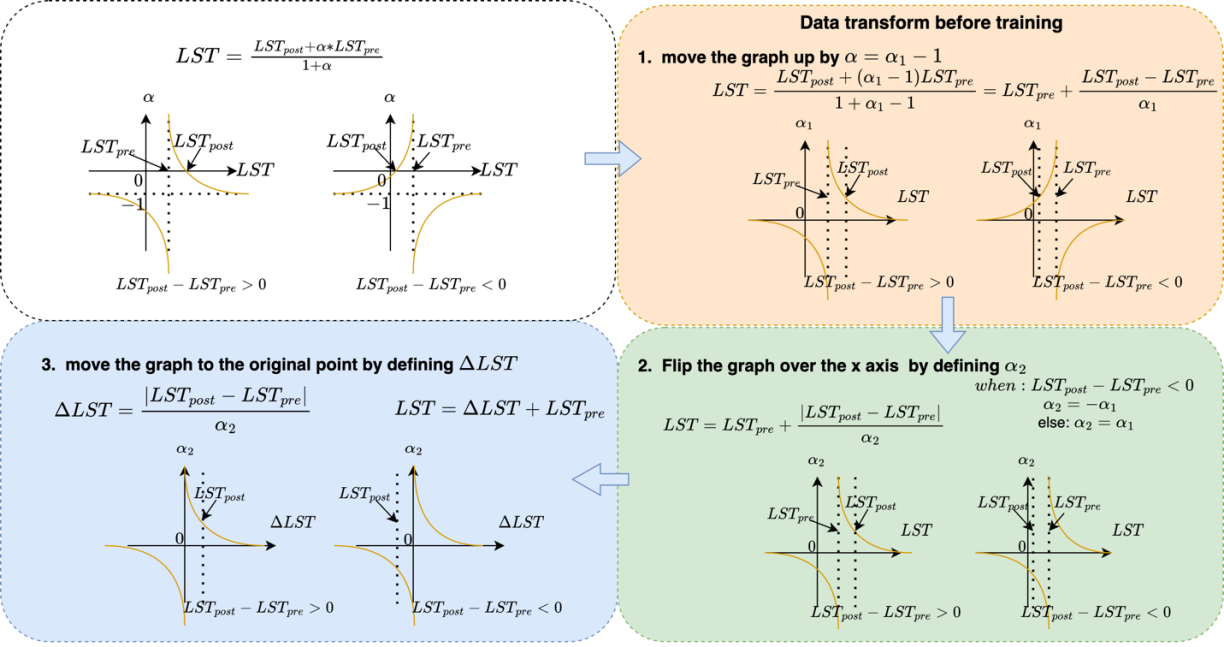
使用真实数据训练的多层感知器模型可以有效捕捉数据分布，并构建一个潜在特征空间，从而根据特征相似性进行准确预测。该模型解决了 U-STFM 原始加权函数中存在的误差敏感性问题。建立稳定的特征空间是训练人工模型的重要前提。要训练 RatioNet，数据必须经过三个步骤的转换过程，才能将这些发散图转换为稳定的特征空间。更多详情可参见图 8。

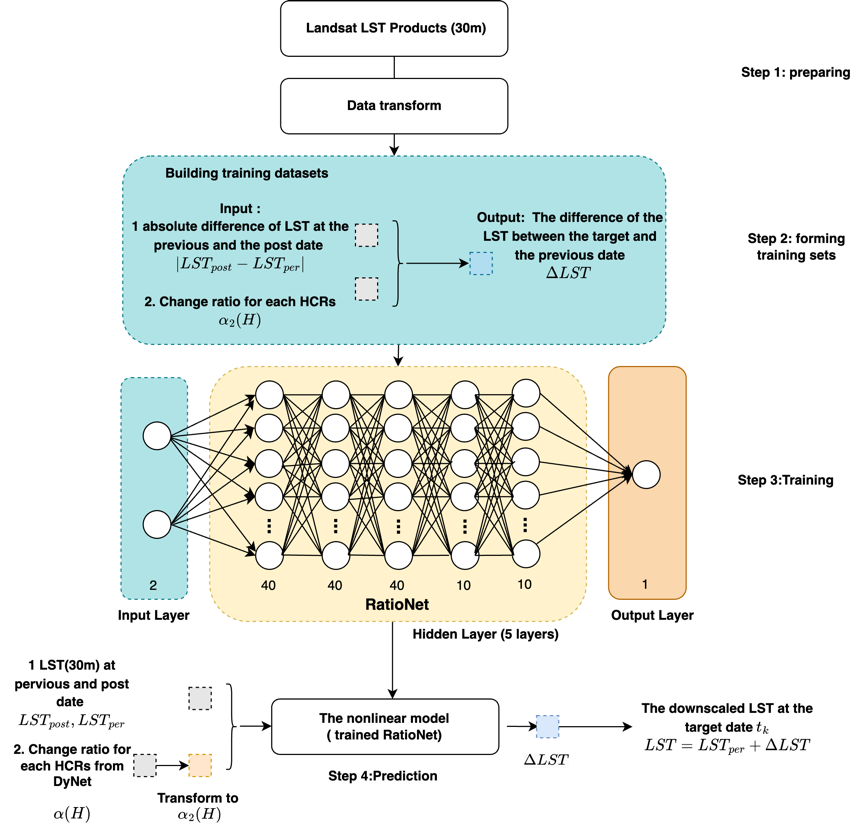
RatioNet的结构和训练过程如图 9所示。

利用I-USTFM 预测每日高分辨率 LST

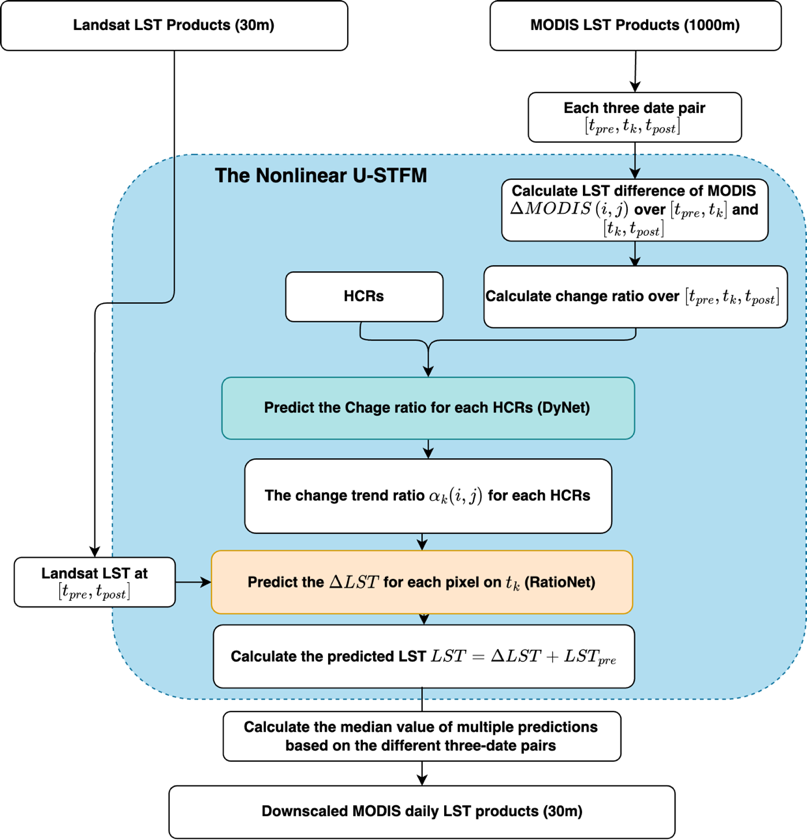
在预测阶段，从时间序列MODIS LST产品中整理出目标日期的多个三日期对。在每个日期对中，计算MODIS时间变化率作为DyNet的输入。DyNet将预测结果作为其输出。然后，根据第 3.3.2 节中提到的数据转换方法，将转换为作为RatioNet的输入。RatioNet提供了对的预测，然后根据计算出精细分辨率下的最终结构LST。根据这一过程，每个三日期对都能提供目标日期的LST预测值。像素级计算的中值提供了最终的LST预测值。预测过程如图 10所示。

评估

在本研究中，采用定性和定量评估方法对模式预报地表温度的效果进行了评估。每次预报都使用空间分辨率为 30 米的陆地卫星地表温度数据作为地面实况。在八个日期中共有六个可信日期。每天对不同的三日期组合组进行评估；例如，2001 年 11 月 20 日就有 12 个三日期组合组。通过对比和检查预期的和实际的 LST 图像对可视化的影响，对模型融合进行了定性评估。在定量评估中，使用了峰值信噪比（PSNR）、相关系数（CC）、均方根误差（RMSE）和平均绝对误差（MAE）。PSNR 是全参考图像的图像质量评价指标。CC值的有效范围介于（-1，1）之间；值越接近 1，表明融合结果越好。更好的预测与更高的PSNR 值、更低的RMSE值和MAE值相关。所有定量评价指标均使用scikit-learn模块中的函数计算。

试验结果及讨论

DyNet 和 RatioNet 的训练过程

使用小批量随机梯度下降算法，可以轻松训练DyNet和RatioNet。图 11显示了训练过程中 500 个历时的损失变化。对于DyNet，测试损失值在 100 个历时后趋于平缓，没有出现过拟合的迹象。测试损失高于训练损失，这表明基本解混过程的难度很大。这可能与训练的批量大小有关。DyNet使用两个动态层来预测每个HCR的变化率，因此建议使用较大的批量。每个批次的平均值被计算为损失。批量越大，就会有越多的MODIS像素参与形成解混过程，损失值也就越接近使用整个验证数据集计算出的地面真实损失。RatioNet的损失图是平滑的，表明根据第4.3.2节所述的数据转换改变特征空间后，网络的学习过程更加容易。

云雾遮挡下的 LST 预测

云层效应是 LST 产品噪音的主要来源。云层温度明显低于地面温度。在我们的数据集中，2000 年 11 月 1 日的数据部分被云层覆盖。因此，我们对模型预测包含噪声（本例中为云层）的日期的 LST 性能进行了评估。

图 12显示了使用DyNet模型预测的每个同质变化区域(HCR)的变化率。在预测 2000 年 11 月 1 日的陆地表面温度时，共考虑了六组三个日期的组合。该图展示了DyNet模型在不同目标日期的一致表现，同时保持了统一的参数。值得注意的是，每个HCR的实际变化率范围可以包含任何数字，因为没有特定的范围被定义为基本事实。在预测过程中，整个图像被剪切成 256 × 256 像素的大小，作为模型的输入。每个批次对该特定批次所涵盖的HCR的变化率进行预测。因此，方框图代表了每个HCR的多个预测值，这些预测值的中值被用作最终的变化率。计算均方根误差（RMSE）是为了评估变化率预测值与地面实况值之间的差异。考虑到不同目标日期的变化率存在差异，DyNet模型的总体性能令人满意。

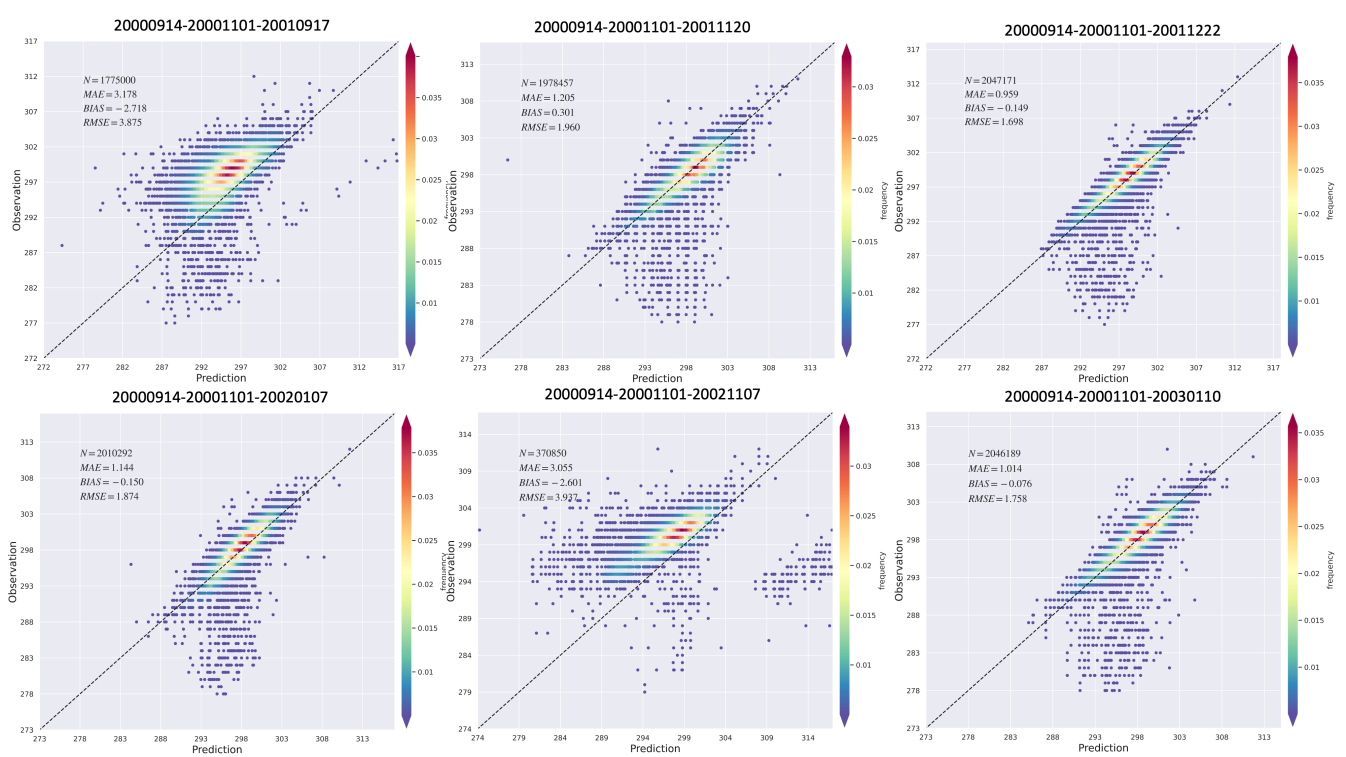
DyNet对各HCR变化率的预测：红色叉号代表地面实况，不同海滩多次预测的中值被用作各HCR变化率的最终预测值

表 2和图 13列出了每个三日期组对 2000年11月1日LST的最终预测结果。预测误差主要有两个原因。首先，它源于DyNet模型预测每个HCR变化率的准确性。例如，在20000914-20001101-20010917 案例中，DyNet预测的均方根误差(RMSE)达到最高值1.579。因此，LST对这一特定日期三元组预测的最终均方根误差达到了3.875。其次，预测误差受基线长度的影响，基线长度表示前一个日期和后一个日期之间的LST差值。如图 3所示，基线长度越小，压缩的数据空间就越接近数值，从而导致RatioNet模型的预测误差越大。例如，考虑 20000914-20001101-20021107 的情况。DyNet 预测的 RMSE 相对较小，为 0.864。但是，该案例的基线长度为 3.015，表 RatioNet的预测不确定性更高。

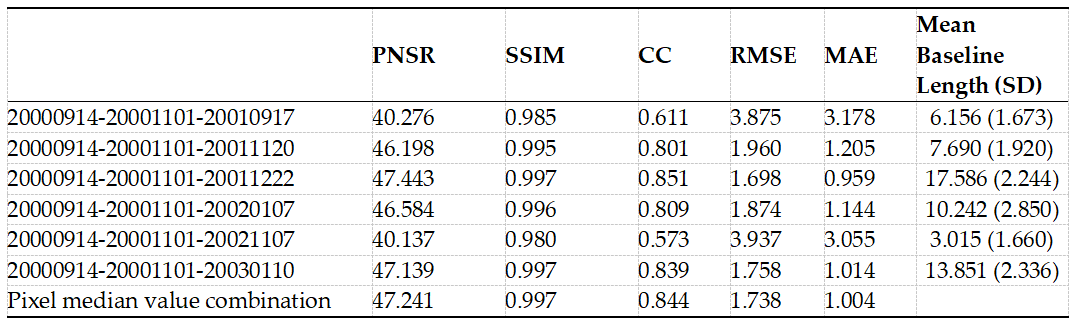
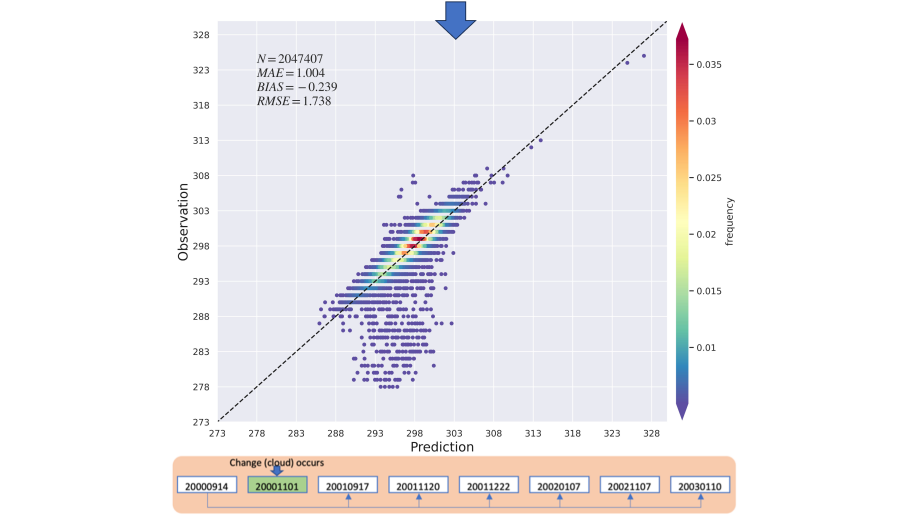
表2：基于非线性U-STFM（DyNet+RatioNet）对每对日期的 30 米分辨率LST预测

在实际的应用过程中，DyNet和RatioNet因基线较短而积累的误差可以通过像素级中值组合得到缓解。图 13显示，1:1中值组合图能有效过滤掉不准确的预测，从而提高准确率。

用不同的三个日期对预测2000年11月1日LST的 1:1 图（左）和最终组合预测结果（像素级的中值）

如图 14c中红圈所示，2000年11月1日Landsat观测到的实际陆地表面温度受云层的部分影响。然而，图 14a所示的MODIS数据没有捕捉到这部分云层信号，导致图 14b所示的非线性U-STFM模型预测中没有云层指示。由于云覆盖区域的LST值是根据被云覆盖的相同HCR内的变化率填充的，因此在 1:1 图（图 14d）和 RMSE 图像（图 14d）中也可以观察到云效应的影响。

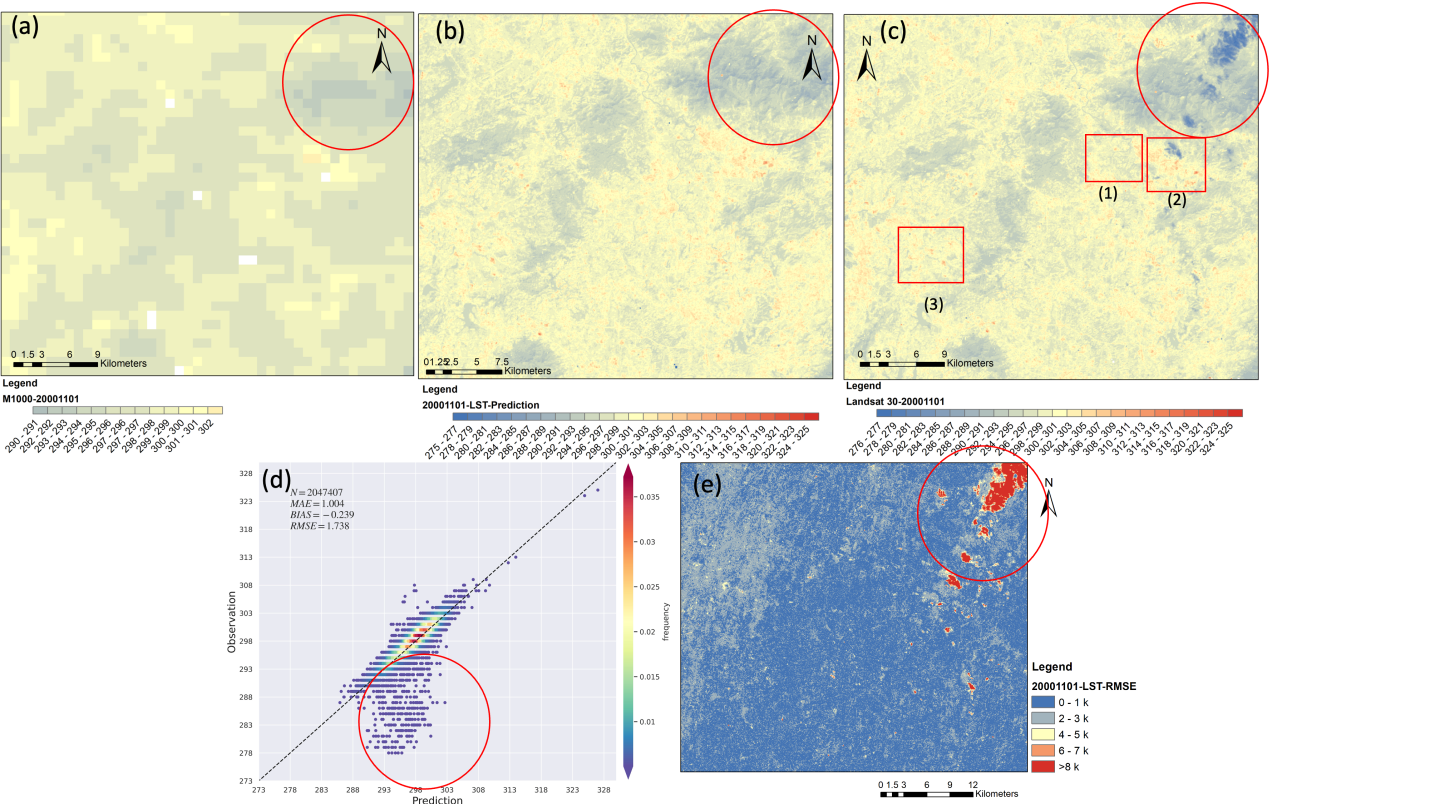
根据多个三重日期组合得出的最终预测结果（2000年11月1日）。(a) 2000 年11月1日的原始MODIS LST；(b)我们的模型预测；(c) Landsat LST；(d)我们的模型预测与Landsat LST之间的1:1图；(e)我们的模型预测与Landsat LST之间的均方根误差图。图15中的（1）-（3）为子区域

为了评估模型检测微妙信号的能力，我们选择了热点和冷点作为参考点。图 15显示，模型成功捕捉到了热点，即区域1和区域2中的红点。此外，模型还准确识别出了区域3冷屋顶上太阳能电池板的存在。

与 STARFM、ESTARFM 和原始 U-STFM 比较

与 STARFM、ESTARFM 和原始 U-STFM 相比，I-USTFM 性能更优，表现出更高的峰值信噪比 (PNSR) 值和更低的均方根误差 (RMSE) 值。详细结果见表 3。图 23 所示的均方根误差图显示，没有任何特定土地覆被类型的均方根误差值明显更高。这表明该模型并没有偏向特定的土地覆被类型。此外，图 23还表明，I-USTFM 有能力自动填补因目标日期 MODIS 数据缺失而造成的云差距。这是通过采用聚类算法定义 HCR 实现的。此外，还可利用属于同一 HCR 类别的其他 MODIS 像素来估算云区下的变化率。

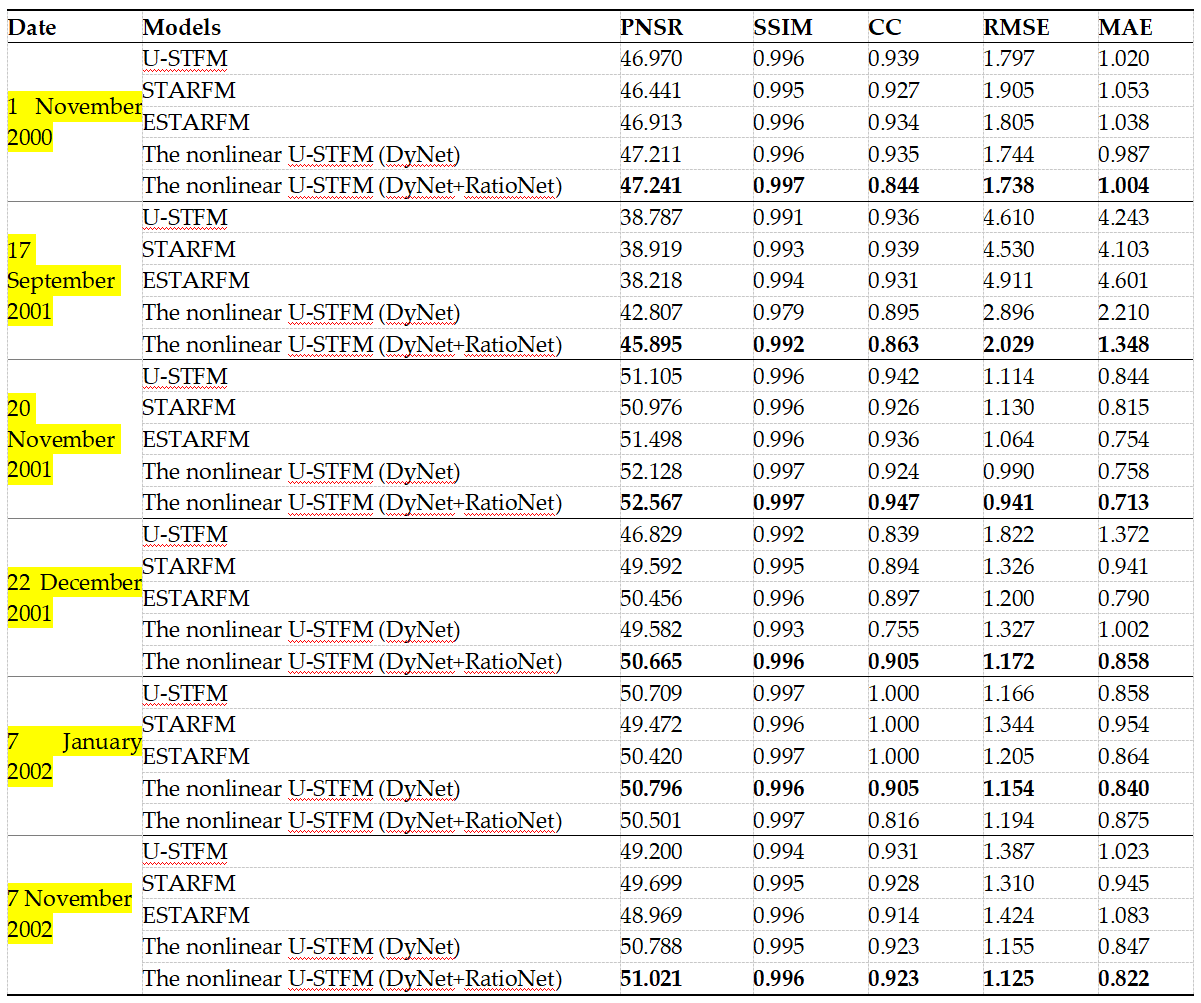
表 3I-USTFM 与 STARFM、ESTARFM 和原始 U-STFM 的比较，粗体值代表每组中表现最好的模型

2001年9月17日STARFM、ESTARFM和U-STFM的RMSE值差异很大，这可能是由于2000年11月1日的云层效应造成的。由于用于预测 2001年9 月17日的三个日期对中有一半包含2000年11月1日的图像，这对 STARFM、ESTARFM 和 U-STFM 的加权函数影响很大。另一个影响因素可能是每个模型所使用的处理单元。STARFM 和 ESTARFM 在像素级别上运行，考虑周围的相似像素。相比之下，UTFM 采用的是由分割算法定义的更大处理单元，从而产生局部区域。I-USTFM 的处理单元最大，由集群定义，有助于减少预测的不确定性。

I-USTFM与 STARFM、ESTARFM 和 U-STFM 预测 RMSE 的比较

结论

陆地表面温度（LST）在各种地理物理过程模拟模型中起着至关重要的作用。近年来，将来自多个卫星平台的高空间分辨率和时间分辨率 LST 数据结合起来的方法受到了广泛关注。为实现这一目标，时空图像融合模型已成为一种有前途的降尺度方法。以往的研究已经证明了基于解混的融合模型（如 U-STFM）通过从时间序列数据中提取特征来捕捉土地覆被变化的有效性。这些模型在降尺度陆地表面反射率和海洋颜色产品等应用中取得了显著成功。然而，在提高原始线性解混函数和小解混内含物理论加权函数的准确性方面仍然存在挑战，特别是在处理 LST 快速变化和降尺度过程中的抗噪声能力时。

为了应对这些挑战，我们引入了一种名为I-USTFM 的 U-STFM 升级版本，其中包含一个深度学习模型。原有的解混频和加权函数被两个深度学习组件所取代： DyNet 和 RatioNet。采用了动态层和特征空间转换技术，即使在数据集相对较小的情况下，也能促进这些网络的训练。

在研究中，我们选择了粤港澳大湾区的一部分作为研究区域，面积约为 1843 平方公里。利用 Landsat-7 和 Landsat LST 30 m 产品将 MODIS 每日数据的分辨率从 1000 m 降到 30 m。

训练过程结束后，结果表明，统一解混网络（DyNet）能有效解混不同目标时间的 MODIS 像素，并随着高变化率（HCR）内含物数量的增加而降低均方根误差（RMSE）新的加权网络（RatioNet）成功地降低了解混过程中存在噪声时的均方根误差。与理论加权函数相比，RatioNet 加入了更多来自真实数据分布和样本相似性的特征，从而增强了模型的鲁棒性。我们还评估了I-USTFM 在受云层影响的日期和 LST 变化方面的整体性能。在对照实验中，新模型的表现优于 STARFM、ESTARFM 和原始 U-STFM 等经典方法，获得了最高的准确率。

与大多数将特征提取和建模作为黑盒子结合起来的端到端深度学习网络不同，本研究中开发的模型将网络与原始的 STFM 模型集成在一起，从而便于解释。此外，预训练网络可以提高预测速度，使其适用于在线实时应用。为了拓展这项研究，使用来自多个地区的不同数据源训练新开发的模型并随后评估其在全球范围内的泛化能力将大有裨益。