$$ \newcommand{\bone}{\mathbf{1}} \newcommand{\bbeta}{\mathbf{\beta}} \newcommand{\bdelta}{\mathbf{\delta}} \newcommand{\bepsilon}{\mathbf{\epsilon}} \newcommand{\blambda}{\mathbf{\lambda}} \newcommand{\bomega}{\mathbf{\omega}} \newcommand{\bpi}{\mathbf{\pi}} \newcommand{\bphi}{\mathbf{\phi}} \newcommand{\bvphi}{\mathbf{\varphi}} \newcommand{\bpsi}{\mathbf{\psi}} \newcommand{\bsigma}{\mathbf{\sigma}} \newcommand{\btheta}{\mathbf{\theta}} \newcommand{\btau}{\mathbf{\tau}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bb}{\mathbf{b}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\boldf}{\mathbf{f}} \newcommand{\bg}{\mathbf{g}} \newcommand{\bh}{\mathbf{h}} \newcommand{\bi}{\mathbf{i}} \newcommand{\bj}{\mathbf{j}} \newcommand{\bk}{\mathbf{k}} \newcommand{\bell}{\mathbf{\ell}} \newcommand{\bm}{\mathbf{m}} \newcommand{\bn}{\mathbf{n}} \newcommand{\bo}{\mathbf{o}} \newcommand{\bp}{\mathbf{p}} \newcommand{\bq}{\mathbf{q}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bt}{\mathbf{t}} \newcommand{\bu}{\mathbf{u}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\bA}{\mathbf{A}} \newcommand{\bB}{\mathbf{B}} \newcommand{\bC}{\mathbf{C}} \newcommand{\bD}{\mathbf{D}} \newcommand{\bE}{\mathbf{E}} \newcommand{\bF}{\mathbf{F}} \newcommand{\bG}{\mathbf{G}} \newcommand{\bH}{\mathbf{H}} \newcommand{\bI}{\mathbf{I}} \newcommand{\bJ}{\mathbf{J}} \newcommand{\bK}{\mathbf{K}} \newcommand{\bL}{\mathbf{L}} \newcommand{\bM}{\mathbf{M}} \newcommand{\bN}{\mathbf{N}} \newcommand{\bP}{\mathbf{P}} \newcommand{\bQ}{\mathbf{Q}} \newcommand{\bR}{\mathbf{R}} \newcommand{\bS}{\mathbf{S}} \newcommand{\bT}{\mathbf{T}} \newcommand{\bU}{\mathbf{U}} \newcommand{\bV}{\mathbf{V}} \newcommand{\bW}{\mathbf{W}} \newcommand{\bX}{\mathbf{X}} \newcommand{\bY}{\mathbf{Y}} \newcommand{\bZ}{\mathbf{Z}} \newcommand{\bsa}{\boldsymbol{a}} \newcommand{\bsb}{\boldsymbol{b}} \newcommand{\bsc}{\boldsymbol{c}} \newcommand{\bsd}{\boldsymbol{d}} \newcommand{\bse}{\boldsymbol{e}} \newcommand{\bsoldf}{\boldsymbol{f}} \newcommand{\bsg}{\boldsymbol{g}} \newcommand{\bsh}{\boldsymbol{h}} \newcommand{\bsi}{\boldsymbol{i}} \newcommand{\bsj}{\boldsymbol{j}} \newcommand{\bsk}{\boldsymbol{k}} \newcommand{\bsell}{\boldsymbol{\ell}} \newcommand{\bsm}{\boldsymbol{m}} \newcommand{\bsn}{\boldsymbol{n}} \newcommand{\bso}{\boldsymbol{o}} \newcommand{\bsp}{\boldsymbol{p}} \newcommand{\bsq}{\boldsymbol{q}} \newcommand{\bsr}{\boldsymbol{r}} \newcommand{\bss}{\boldsymbol{s}} \newcommand{\bst}{\boldsymbol{t}} \newcommand{\bsu}{\boldsymbol{u}} \newcommand{\bsv}{\boldsymbol{v}} \newcommand{\bsw}{\boldsymbol{w}} \newcommand{\bsx}{\boldsymbol{x}} \newcommand{\bsy}{\boldsymbol{y}} \newcommand{\bsz}{\boldsymbol{z}} \newcommand{\bsA}{\boldsymbol{A}} \newcommand{\bsB}{\boldsymbol{B}} \newcommand{\bsC}{\boldsymbol{C}} \newcommand{\bsD}{\boldsymbol{D}} \newcommand{\bsE}{\boldsymbol{E}} \newcommand{\bsF}{\boldsymbol{F}} \newcommand{\bsG}{\boldsymbol{G}} \newcommand{\bsH}{\boldsymbol{H}} \newcommand{\bsI}{\boldsymbol{I}} \newcommand{\bsJ}{\boldsymbol{J}} \newcommand{\bsK}{\boldsymbol{K}} \newcommand{\bsL}{\boldsymbol{L}} \newcommand{\bsM}{\boldsymbol{M}} \newcommand{\bsN}{\boldsymbol{N}} \newcommand{\bsP}{\boldsymbol{P}} \newcommand{\bsQ}{\boldsymbol{Q}} \newcommand{\bsR}{\boldsymbol{R}} \newcommand{\bsS}{\boldsymbol{S}} \newcommand{\bsT}{\boldsymbol{T}} \newcommand{\bsU}{\boldsymbol{U}} \newcommand{\bsV}{\boldsymbol{V}} \newcommand{\bsW}{\boldsymbol{W}} \newcommand{\bsX}{\boldsymbol{X}} \newcommand{\bsY}{\boldsymbol{Y}} \newcommand{\bsZ}{\boldsymbol{Z}} \newcommand{\calA}{\mathcal{A}} \newcommand{\calB}{\mathcal{B}} \newcommand{\calC}{\mathcal{C}} \newcommand{\calD}{\mathcal{D}} \newcommand{\calE}{\mathcal{E}} \newcommand{\calF}{\mathcal{F}} \newcommand{\calG}{\mathcal{G}} \newcommand{\calH}{\mathcal{H}} \newcommand{\calI}{\mathcal{I}} \newcommand{\calJ}{\mathcal{J}} \newcommand{\calK}{\mathcal{K}} \newcommand{\calL}{\mathcal{L}} \newcommand{\calM}{\mathcal{M}} \newcommand{\calN}{\mathcal{N}} \newcommand{\calO}{\mathcal{O}} \newcommand{\calP}{\mathcal{P}} \newcommand{\calQ}{\mathcal{Q}} \newcommand{\calR}{\mathcal{R}} \newcommand{\calS}{\mathcal{S}} \newcommand{\calT}{\mathcal{T}} \newcommand{\calU}{\mathcal{U}} \newcommand{\calV}{\mathcal{V}} \newcommand{\calW}{\mathcal{W}} \newcommand{\calX}{\mathcal{X}} \newcommand{\calY}{\mathcal{Y}} \newcommand{\calZ}{\mathcal{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\F}{\mathbb{F}} \newcommand{\Q}{\mathbb{Q}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \newcommand{\nnz}[1]{\mbox{nnz}(#1)} \newcommand{\dotprod}[2]{\langle #1, #2 \rangle} \newcommand{\ignore}[1]{} \let\Pr\relax \DeclareMathOperator*{\Pr}{\mathbf{Pr}} \newcommand{\E}{\mathbb{E}} \DeclareMathOperator*{\Ex}{\mathbf{E}} \DeclareMathOperator*{\Var}{\mathbf{Var}} \DeclareMathOperator*{\Cov}{\mathbf{Cov}} \DeclareMathOperator*{\stddev}{\mathbf{stddev}} \DeclareMathOperator*{\avg}{avg} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\dist}{dist} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\spn}{span} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\codim}{codim} \DeclareMathOperator{\diag}{diag} \newcommand{\PTIME}{\mathsf{P}} \newcommand{\LOGSPACE}{\mathsf{L}} \newcommand{\ZPP}{\mathsf{ZPP}} \newcommand{\RP}{\mathsf{RP}} \newcommand{\BPP}{\mathsf{BPP}} \newcommand{\P}{\mathsf{P}} \newcommand{\NP}{\mathsf{NP}} \newcommand{\TC}{\mathsf{TC}} \newcommand{\AC}{\mathsf{AC}} \newcommand{\SC}{\mathsf{SC}} \newcommand{\SZK}{\mathsf{SZK}} \newcommand{\AM}{\mathsf{AM}} \newcommand{\IP}{\mathsf{IP}} \newcommand{\PSPACE}{\mathsf{PSPACE}} \newcommand{\EXP}{\mathsf{EXP}} \newcommand{\MIP}{\mathsf{MIP}} \newcommand{\NEXP}{\mathsf{NEXP}} \newcommand{\BQP}{\mathsf{BQP}} \newcommand{\distP}{\mathsf{dist\textbf{P}}} \newcommand{\distNP}{\mathsf{dist\textbf{NP}}} \newcommand{\eps}{\epsilon} \newcommand{\lam}{\lambda} \newcommand{\dleta}{\delta} \newcommand{\simga}{\sigma} \newcommand{\vphi}{\varphi} \newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\wt}[1]{\widetilde{#1}} \newcommand{\wh}[1]{\widehat{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\ot}{\otimes} \newcommand{\zo}{\{0,1\}} \newcommand{\co}{:} %\newcommand{\co}{\colon} \newcommand{\bdry}{\partial} \newcommand{\grad}{\nabla} \newcommand{\transp}{^\intercal} \newcommand{\inv}{^{-1}} \newcommand{\symmdiff}{\triangle} \newcommand{\symdiff}{\symmdiff} \newcommand{\half}{\tfrac{1}{2}} \newcommand{\mathbbm}{\Bbb} \newcommand{\bbone}{\mathbbm 1} \newcommand{\Id}{\bbone} \newcommand{\SAT}{\mathsf{SAT}} \newcommand{\bcalG}{\boldsymbol{\calG}} \newcommand{\calbG}{\bcalG} \newcommand{\bcalX}{\boldsymbol{\calX}} \newcommand{\calbX}{\bcalX} \newcommand{\bcalY}{\boldsymbol{\calY}} \newcommand{\calbY}{\bcalY} \newcommand{\bcalZ}{\boldsymbol{\calZ}} \newcommand{\calbZ}{\bcalZ} $$

基于光学微波特征融合的典型经济作物提取

Created in March 10, 2024 by Shanxin Guo

2024   ·   machine-learning   remote-sensing

post.cover
深圳湾夜景

研究背景

新疆是我国西北干旱半干旱地区的主要农业区。由于气候干燥，新疆的农业生产几乎完全依赖灌溉，进一步加剧了水资源匮乏问题。新疆是我国棉花的主要产区，种植面积大且品质优良，是国内棉花供给的重要支柱。2017年，新疆棉花种植面积占全国比重超过60%，产量占全国比重超过70%。然而，棉花种植需要大量水源灌溉，加速了土地荒漠化的进程。近年来，新疆部分地区通过农业结构调整，实施“退白扩红”战略，大量种植辣椒和番茄，种植结构更加复杂，因此需要更加及时、精确的农作物种类分布制图。这些信息对于水资源管理和环境承载力评估至关重要。

遥感技术因其宏观、准确、及时的特点，已被广泛应用于大范围农作物种植面积和长势监测中，为农业生产管理和粮食政策制定提供了重要参考。然而，传统光学遥感影像受云雨天气影响，难以获取连续的时间序列数据，尤其是在作物生长关键期。此外，对于具有相似物候周期的作物，仅依靠光谱信息难以区分。

星载合成孔径雷达（SAR）遥感具有全天时、全天候、覆盖范围广、穿透能力强的特点，能够反映植被的结构特征和介电特性，已逐渐成为遥感作物分类的重要工具。研究表明，增加SAR极化通道或使用多时相数据可以显著提高作物分类精度。然而，SAR影像受相干斑噪声影响较大，现有技术对后向散射强度的相干斑抑制效果有限，容易模糊强散射体与周边低相干区域。此外，大部分研究仅关注雷达后向散射强度，未充分评估SAR影像其他特征在作物分类中的作用。

为克服光学遥感影像受云影响的不足，并结合SAR影像的优势，本研究提出了一种集成Sentinel-1和Sentinel-2特征的方法，对新疆巴州地区典型绿洲农业区进行作物分类制图。研究采用SHP-DSI方法对SAR数据进行相干斑抑制，并提取多种SAR和InSAR特征。同时，提取Sentinel-2的红边波段和红边指数，与常规多光谱特征结合，提升作物分类精度。通过随机森林算法对特征重要性排序，并采用递归特征增量（RFI）方法筛选最优特征组合，最终实现高精度作物分类。

模型方法介绍

本研究中使用的工作流程如图 3.6.2所示。

实验流程
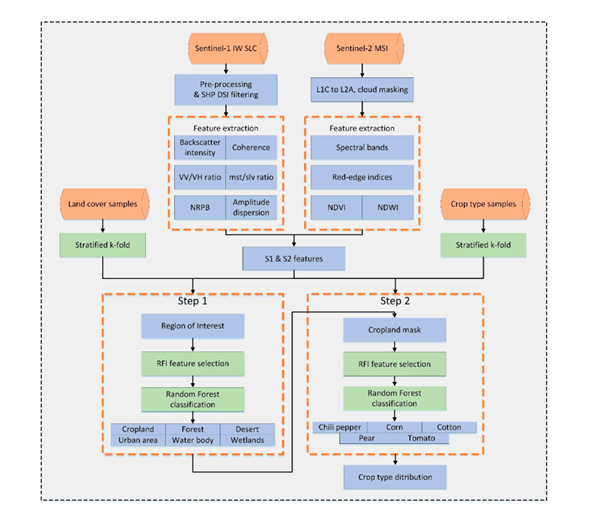
  1. 基于Sentinel-1数据提取SAR和InSAR特征 对时间序列Sentinel-1 IW SLC数据进行预处理，包括精配准、镶嵌、裁剪。为提高SAR和InSAR特征的信噪比，基于Gamma置信区间判别从时序SAR数据中提取统计同质像元（SHP），并采用SHP-DSI算法进行相干斑滤波，在此基础上提取SAR和InSAR特征。
  2. 基于Sentinel-2数据提取多光谱特征 对多时相Sentinel-2数据进行预处理，采用sen2cor软件将L1C级Top of Atmosphere (TOA)产品转换为L2A级产品表面反射率(surface reflectance)，提取10米、20米分辨率的所有谱段（包括B2, B3, B4, B5 B6, B7, B8, B8A, B11, B12）；并计算植被指数、水体指数、红边指数等
  3. 雷达和光学特征融合 基于随机森林（Random Forest，RF）算法对所有特征进行重要性排序，在此基础上采用递归特征增加（Recursive Feature Increment，RFI）方法选取最优特征组合，进行土地覆盖分类，获取农田掩膜；在农田掩膜范围内，进行作物分类，得到作物分类制图。

试验结果

采用基于统计同质像素（SHP）的SHP-DSI 算法对SAR影像进行相干斑抑制和相干系数估计，结果如下：

SAR后向散射强度图 (a)原始强度图； (b) Refined Lee算法滤波后强度图；(c) SHP-DSI算法滤波后强度图
干涉相干系数 (a) 常规7*7滑窗估计的干涉相干系数;(b) SHP-DSI 算法估计的干涉相干系数

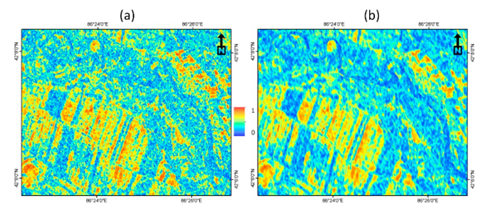
表3.6.6采用不同方法处理后的SAR&InSAR特征进行作物分类的精度

  Mean OA Kappa Coefficient F1-score chili F1-score corn F1-score cotton F1-score pear F1-score tomato
Original 60.20% 0.48 0.55 0.33 0.67 0.72 0.58
Refined Lee 73.21% 0.65 0.66 0.52 0.80 0.83 0.74
SHP DSI 79.46% 0.73 0.75 0.60 0.88 0.86 0.77

从表3.6.6中可以看到，采用SHP-DSI算法较原始数据和常规Refined Lee算法滤波后提取的SAR和InSAR特征在作物分类制图中显著提高了精度，无论是总体精度（OA）、Kappa系数，还是每一个作物种类的F1-sore都有显著提高。采用随机森林算法进行一级类分类以提取农田，并采用分层交叉验证（K=10份）方法对总体精度和农田提取精度进行验证，结果如下：

(a) 土地覆盖分类结果；(b) 农田掩膜
雷达和光学特征集成获取的作物种类制图

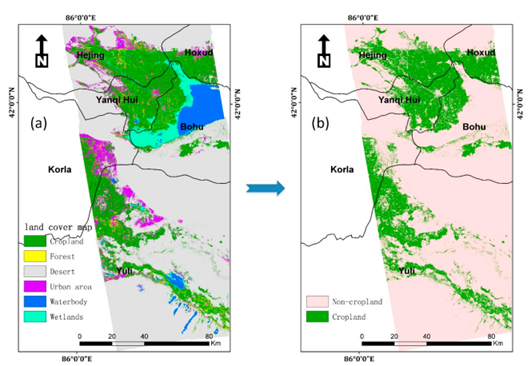
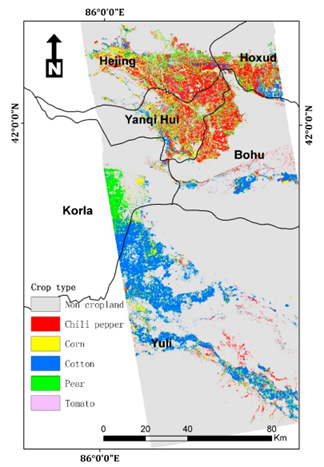
对比只使用SAR特征，只使用光学特征，以及SAR和光学特征的最优组合分别进行作物分类制图，精度对比如下：

表 3.6.9分别采用Sentinel-1、Sentinel-2常规多光谱特征、Sentinel-2包括红边特征在内的所有光学特征、Sentinel-1&2集成特征的作物分类制图精度对比

  Number of features Mean OA Kappa Coefficient
Sentinel-1 133 79.46% 0.73
Sentinel-2 without red-edge features 58 82.37% 0.77
Sentinel-2 104 85.43% 0.81
Sentinel-1 & Sentinel-2 113 86.98% 0.83

表3.6.9说明，Sentinel-2的红边特征对比常规多光谱特征，将作物分类的OA提高了3.06%,Kappa系数提高了0.04；Sentinel-1雷达和Sentinel-2光学特征融合后，总体精度(OA)和Kappa系数比单独使用雷达或光学特征都有显著提高。

对比分别采用Sentinel-1、Sentinel-2常规多光谱特征、Sentinel-2包括红边特征在内的所有光学特征、Sentinel-1&2集成特征的每种作物类别的提取精度如图3.6.7所示。

不同特征组合下不同种类作物的提取精度对比

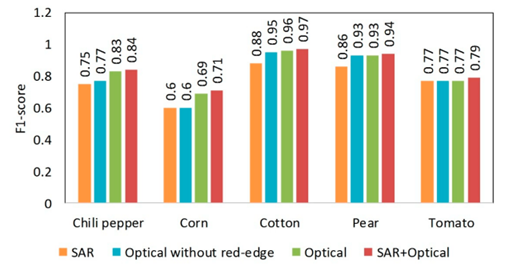
从图3.6.7中本研究可以发现，对于辣椒和玉米，红边特征对提取精度的提高较显著；对于棉花和香梨，只采用Sentinel-1雷达特征时，各自的提取精度已经很高，Sentinel-2多光谱特征的加入又进一步提高了提取精度；对于番茄的提取，采用雷达特征、常规多光谱特征、红边特征的提取精度是一样的，雷达和光学特征的集成才显著提高了提取精度。查看每种作物的提取精度对比，共同点是，采用Sentinel-1&2集成特征时，辣椒、玉米、棉花、香梨、番茄每种作物的提取F1-score都是几个特征组合中最高的。

结论

本研究通过西北某小农区的案例研究，提出了一种协同利用 Sentinel-1 和 Sentinel-2 特征进行绿洲作物类型测绘的方法。首先，引入了 SHP DSI 算法，对 SAR 强度进行去斑处理，准确估计干涉测量相干性，提高 SAR 特征的质量。研究表明，在仅使用 SAR 特征的情况下，使用 SHP DSI 方法可使作物分类精度提高 6.25%。从多时态的 Sentinel-1 和 Sentinel-2 图像中得到了多种 SAR 特征和光学特征，包括几种 InSAR 产品和红边光谱波段和指数。其次，根据随机森林分类器的换元重要性，提出了一种递归特征增量特征选择方法，得到 Sentinel-1和 Sentinel-2 特征的最优组合，用于农田提取和作物类型分类。最后，生成了作物分布图，总体精度为 83.22%， kappa 系数为 0.77。对 SAR 和光学特征的贡献进行了深入探讨。在所有 Sentinel-1 特征中,VH 强度所占比例最大,说明 VH 偏振对植被变化的敏感性较好。同时，还注意到 InSAR 的一些产品，如 VH 振幅色散、主从强度比、 4 月上旬的 VV相干性等，揭示了某些作物类型的良好分离性。至于 Sentinel-2 特征，我们证明了在绿洲作物类型测绘中使用红边光谱波段和指数的优点。与仅使用传统光学特征相比，红边特征的加入使作物分类 OA提高了 1.84%。这证明了 Sentinel-2 数据的优越性，因为光谱分辨率的提高。对使用 4 种特征组合的绿洲作物分类性能进行了比较。结果表明， SAR 和光学特征的集成取得了最佳性能。我们认为，时间序列 S1 和 S2 图像的集成具有优势，由于数据的免费、充分和开放政策，可以在绝大多数地区进一步探索用于作物状况监测。

原文链接

Sun, L., Chen, J., Guo, S., Deng, X., & Han, Y. (2020). Integration of Time Series Sentinel-1 and Sentinel-2 Imagery for Crop Type Mapping over Oasis Agricultural Areas. Remote Sensing, 12(158), 1–27.



    Enjoy Reading This Article?

    Here are some more articles you might like to read next:

  • 基于时空融合的MODIS产品降尺度模型-以海表叶绿素为例
  • 面向地表快速变化场景的时空融合的动态神经网络I-USTFM：以地表温度为例
  • 对抗样本噪声的遥感深度学习分类网络模型
  • 快速评估监督学习中常用遥感分类算法的时间效率
  • 基于对抗神经网络ISRGAN的多源遥感数据融合与超分辨模型