$$ \newcommand{\bone}{\mathbf{1}} \newcommand{\bbeta}{\mathbf{\beta}} \newcommand{\bdelta}{\mathbf{\delta}} \newcommand{\bepsilon}{\mathbf{\epsilon}} \newcommand{\blambda}{\mathbf{\lambda}} \newcommand{\bomega}{\mathbf{\omega}} \newcommand{\bpi}{\mathbf{\pi}} \newcommand{\bphi}{\mathbf{\phi}} \newcommand{\bvphi}{\mathbf{\varphi}} \newcommand{\bpsi}{\mathbf{\psi}} \newcommand{\bsigma}{\mathbf{\sigma}} \newcommand{\btheta}{\mathbf{\theta}} \newcommand{\btau}{\mathbf{\tau}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bb}{\mathbf{b}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\boldf}{\mathbf{f}} \newcommand{\bg}{\mathbf{g}} \newcommand{\bh}{\mathbf{h}} \newcommand{\bi}{\mathbf{i}} \newcommand{\bj}{\mathbf{j}} \newcommand{\bk}{\mathbf{k}} \newcommand{\bell}{\mathbf{\ell}} \newcommand{\bm}{\mathbf{m}} \newcommand{\bn}{\mathbf{n}} \newcommand{\bo}{\mathbf{o}} \newcommand{\bp}{\mathbf{p}} \newcommand{\bq}{\mathbf{q}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bt}{\mathbf{t}} \newcommand{\bu}{\mathbf{u}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\bA}{\mathbf{A}} \newcommand{\bB}{\mathbf{B}} \newcommand{\bC}{\mathbf{C}} \newcommand{\bD}{\mathbf{D}} \newcommand{\bE}{\mathbf{E}} \newcommand{\bF}{\mathbf{F}} \newcommand{\bG}{\mathbf{G}} \newcommand{\bH}{\mathbf{H}} \newcommand{\bI}{\mathbf{I}} \newcommand{\bJ}{\mathbf{J}} \newcommand{\bK}{\mathbf{K}} \newcommand{\bL}{\mathbf{L}} \newcommand{\bM}{\mathbf{M}} \newcommand{\bN}{\mathbf{N}} \newcommand{\bP}{\mathbf{P}} \newcommand{\bQ}{\mathbf{Q}} \newcommand{\bR}{\mathbf{R}} \newcommand{\bS}{\mathbf{S}} \newcommand{\bT}{\mathbf{T}} \newcommand{\bU}{\mathbf{U}} \newcommand{\bV}{\mathbf{V}} \newcommand{\bW}{\mathbf{W}} \newcommand{\bX}{\mathbf{X}} \newcommand{\bY}{\mathbf{Y}} \newcommand{\bZ}{\mathbf{Z}} \newcommand{\bsa}{\boldsymbol{a}} \newcommand{\bsb}{\boldsymbol{b}} \newcommand{\bsc}{\boldsymbol{c}} \newcommand{\bsd}{\boldsymbol{d}} \newcommand{\bse}{\boldsymbol{e}} \newcommand{\bsoldf}{\boldsymbol{f}} \newcommand{\bsg}{\boldsymbol{g}} \newcommand{\bsh}{\boldsymbol{h}} \newcommand{\bsi}{\boldsymbol{i}} \newcommand{\bsj}{\boldsymbol{j}} \newcommand{\bsk}{\boldsymbol{k}} \newcommand{\bsell}{\boldsymbol{\ell}} \newcommand{\bsm}{\boldsymbol{m}} \newcommand{\bsn}{\boldsymbol{n}} \newcommand{\bso}{\boldsymbol{o}} \newcommand{\bsp}{\boldsymbol{p}} \newcommand{\bsq}{\boldsymbol{q}} \newcommand{\bsr}{\boldsymbol{r}} \newcommand{\bss}{\boldsymbol{s}} \newcommand{\bst}{\boldsymbol{t}} \newcommand{\bsu}{\boldsymbol{u}} \newcommand{\bsv}{\boldsymbol{v}} \newcommand{\bsw}{\boldsymbol{w}} \newcommand{\bsx}{\boldsymbol{x}} \newcommand{\bsy}{\boldsymbol{y}} \newcommand{\bsz}{\boldsymbol{z}} \newcommand{\bsA}{\boldsymbol{A}} \newcommand{\bsB}{\boldsymbol{B}} \newcommand{\bsC}{\boldsymbol{C}} \newcommand{\bsD}{\boldsymbol{D}} \newcommand{\bsE}{\boldsymbol{E}} \newcommand{\bsF}{\boldsymbol{F}} \newcommand{\bsG}{\boldsymbol{G}} \newcommand{\bsH}{\boldsymbol{H}} \newcommand{\bsI}{\boldsymbol{I}} \newcommand{\bsJ}{\boldsymbol{J}} \newcommand{\bsK}{\boldsymbol{K}} \newcommand{\bsL}{\boldsymbol{L}} \newcommand{\bsM}{\boldsymbol{M}} \newcommand{\bsN}{\boldsymbol{N}} \newcommand{\bsP}{\boldsymbol{P}} \newcommand{\bsQ}{\boldsymbol{Q}} \newcommand{\bsR}{\boldsymbol{R}} \newcommand{\bsS}{\boldsymbol{S}} \newcommand{\bsT}{\boldsymbol{T}} \newcommand{\bsU}{\boldsymbol{U}} \newcommand{\bsV}{\boldsymbol{V}} \newcommand{\bsW}{\boldsymbol{W}} \newcommand{\bsX}{\boldsymbol{X}} \newcommand{\bsY}{\boldsymbol{Y}} \newcommand{\bsZ}{\boldsymbol{Z}} \newcommand{\calA}{\mathcal{A}} \newcommand{\calB}{\mathcal{B}} \newcommand{\calC}{\mathcal{C}} \newcommand{\calD}{\mathcal{D}} \newcommand{\calE}{\mathcal{E}} \newcommand{\calF}{\mathcal{F}} \newcommand{\calG}{\mathcal{G}} \newcommand{\calH}{\mathcal{H}} \newcommand{\calI}{\mathcal{I}} \newcommand{\calJ}{\mathcal{J}} \newcommand{\calK}{\mathcal{K}} \newcommand{\calL}{\mathcal{L}} \newcommand{\calM}{\mathcal{M}} \newcommand{\calN}{\mathcal{N}} \newcommand{\calO}{\mathcal{O}} \newcommand{\calP}{\mathcal{P}} \newcommand{\calQ}{\mathcal{Q}} \newcommand{\calR}{\mathcal{R}} \newcommand{\calS}{\mathcal{S}} \newcommand{\calT}{\mathcal{T}} \newcommand{\calU}{\mathcal{U}} \newcommand{\calV}{\mathcal{V}} \newcommand{\calW}{\mathcal{W}} \newcommand{\calX}{\mathcal{X}} \newcommand{\calY}{\mathcal{Y}} \newcommand{\calZ}{\mathcal{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\F}{\mathbb{F}} \newcommand{\Q}{\mathbb{Q}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \newcommand{\nnz}[1]{\mbox{nnz}(#1)} \newcommand{\dotprod}[2]{\langle #1, #2 \rangle} \newcommand{\ignore}[1]{} \let\Pr\relax \DeclareMathOperator*{\Pr}{\mathbf{Pr}} \newcommand{\E}{\mathbb{E}} \DeclareMathOperator*{\Ex}{\mathbf{E}} \DeclareMathOperator*{\Var}{\mathbf{Var}} \DeclareMathOperator*{\Cov}{\mathbf{Cov}} \DeclareMathOperator*{\stddev}{\mathbf{stddev}} \DeclareMathOperator*{\avg}{avg} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\dist}{dist} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\spn}{span} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\codim}{codim} \DeclareMathOperator{\diag}{diag} \newcommand{\PTIME}{\mathsf{P}} \newcommand{\LOGSPACE}{\mathsf{L}} \newcommand{\ZPP}{\mathsf{ZPP}} \newcommand{\RP}{\mathsf{RP}} \newcommand{\BPP}{\mathsf{BPP}} \newcommand{\P}{\mathsf{P}} \newcommand{\NP}{\mathsf{NP}} \newcommand{\TC}{\mathsf{TC}} \newcommand{\AC}{\mathsf{AC}} \newcommand{\SC}{\mathsf{SC}} \newcommand{\SZK}{\mathsf{SZK}} \newcommand{\AM}{\mathsf{AM}} \newcommand{\IP}{\mathsf{IP}} \newcommand{\PSPACE}{\mathsf{PSPACE}} \newcommand{\EXP}{\mathsf{EXP}} \newcommand{\MIP}{\mathsf{MIP}} \newcommand{\NEXP}{\mathsf{NEXP}} \newcommand{\BQP}{\mathsf{BQP}} \newcommand{\distP}{\mathsf{dist\textbf{P}}} \newcommand{\distNP}{\mathsf{dist\textbf{NP}}} \newcommand{\eps}{\epsilon} \newcommand{\lam}{\lambda} \newcommand{\dleta}{\delta} \newcommand{\simga}{\sigma} \newcommand{\vphi}{\varphi} \newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\wt}[1]{\widetilde{#1}} \newcommand{\wh}[1]{\widehat{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\ot}{\otimes} \newcommand{\zo}{\{0,1\}} \newcommand{\co}{:} %\newcommand{\co}{\colon} \newcommand{\bdry}{\partial} \newcommand{\grad}{\nabla} \newcommand{\transp}{^\intercal} \newcommand{\inv}{^{-1}} \newcommand{\symmdiff}{\triangle} \newcommand{\symdiff}{\symmdiff} \newcommand{\half}{\tfrac{1}{2}} \newcommand{\mathbbm}{\Bbb} \newcommand{\bbone}{\mathbbm 1} \newcommand{\Id}{\bbone} \newcommand{\SAT}{\mathsf{SAT}} \newcommand{\bcalG}{\boldsymbol{\calG}} \newcommand{\calbG}{\bcalG} \newcommand{\bcalX}{\boldsymbol{\calX}} \newcommand{\calbX}{\bcalX} \newcommand{\bcalY}{\boldsymbol{\calY}} \newcommand{\calbY}{\bcalY} \newcommand{\bcalZ}{\boldsymbol{\calZ}} \newcommand{\calbZ}{\bcalZ} $$

基于对抗神经网络ISRGAN的多源遥感数据融合与超分辨模型

Created in March 07, 2024 by Shanxin Guo

2024   ·   images-fusion   remote-sensing

post.cover
深圳石岩湿地公园

研究背景

详细和准确的土地覆盖和土地利用空间变化信息是地方生态和环境研究的重要基础。为了完成这些任务，需要高空间分辨率的图像来捕捉地球表面的时空动态变化。目前，获取高时空分辨率影像的方法主要有两种：1）多源影像融合模型；2）影像超分辨率模型。

与图像融合模型相比，超分辨模型无需在相近时间内获取同一区域的高空间分辨率影像，因此在计算机视觉和遥感领域的多种场景中具有更强的适用性。

图像超分辨率模型的基本假设是：如果低空间分辨率图像是通过某种重采样过程生成的，那么可以通过重建或从其他高空间分辨率图像中学习，恢复低分辨率图像中缺失的细节。基于这一假设，过去十年中，研究者们致力于准确预测点扩散函数（PSF），即形成低分辨率像素的混合过程。目前主要有三种方法：1）基于插值的方法；2）基于重构的方法；3）基于学习的方法（见表 1）。

首先，插值法是基于一定的数学策略，从相关点计算要恢复的目标点的像素值，其复杂度低，效率高。但是，得到的图像的边缘效果很明显，在插值过程中没有产生新的信息，无法恢复图像的细节。

其次，重构法对成像过程进行建模，整合来自同一场景的不同信息，获得高质量的重构结果。通常这些方法为了提高空间分辨率而牺牲时间分辨率，需要预先配准和大量的算力。

第三，学习法克服了难以确定重建方法的分辨率改进倍数的限制，可以面向单一图像，这是目前超分辨率重建的主要发展方向。在这类方法中，常用的方法有近邻嵌入法、稀疏表示法和深度学习法。

表 1超分辨方法对比

方法大类 模型 基本思想 优点 缺点
插值法 最近邻插值法，二次卷积法，三次卷积法 当前像素值可以用邻近的像素表示 复杂度低，效率高 图像纹理细节无法预测
重构法 联合地图配准，PSF反卷积，稀疏回归法 通过重建技术恢复图像物理性质和特征，使点扩散函数进一步恢复图像细节 融合同一场景的不同信息，得到高质量重建结果 配准需要耗费大量计算时间
学习法 邻域嵌入法，稀疏表达法，贝叶斯网络，SRCNN，SRGAN 通过学习大量图像样本，创建点扩散函数 样本数量较多时生成的图像更接近目标图像，获得更高的PSNR 训练时间长，需要大量数据集，模型泛化能力差

学习法通常需要高度代表性的训练样本来覆盖总体数据的变化。在实际操作中，为了达到这一目标，通常需要收集大量的训练样本。然而，在遥感领域，几乎不可能准备这样的大规模训练样本集，因为遥感数据的变化不仅取决于目标的变化，还受到不同位置和不同卫星传感器的影响。由于这一限制，许多基于学习的方法都局限于某个特定位置和传感器，导致模型在跨区域和跨传感器上的泛化能力不足。这一问题仍然是为不同区域和传感器训练通用超分辨率模型的主要挑战。

近年来，随着人工智能特别是基于神经网络的深度学习方法的快速发展，深度学习在处理大样本集并保持良好泛化能力方面展现了显著优势，并在计算机视觉领域得到了广泛应用。在图像超分辨率领域，Dong于2014年首次提出了超分辨率神经网络SRCNN ^[16]^ 。与传统方法相比，该方法在峰值信噪比（PSNR）上表现更优，但当采样率较高时，重建图像会显得过于平滑，导致细节丢失。为了解决这一问题，Ledig等人提出了超分辨率生成对抗网络模型SRGAN，将原始CNN结构替换为GAN ^[17]^ 。作为深度学习领域的最新模型，SRGAN在捕获大样本的高维非线性特征方面表现出许多优势。然而，SRGAN模型在不同位置和传感器的遥感图像上的泛化能力仍有待验证。

在本研究中，我们验证了基于GAN的方法可以提高模型在跨区域和跨传感器上的泛化能力。通过对SRGAN模型进行一些改进，可以实现一次性训练，并将结果应用于不同区域和传感器。本研究的主要贡献如下：

1）在SRGAN的基础上，提出了ISRGAN模型，解决了SRGAN训练不稳定以及模型泛化能力弱的问题；

2）通过计算模型在广东GF1数据集和新疆GF1数据集上的定量指标并进行t检验，验证了模型在跨区域上的普适性；

3）通过计算模型在新疆GF1数据集和新疆Landsat8数据集上的定量指标并进行t检验，验证了模型在跨传感器上的普适性；

4）以应用服务为目标，将超分辨后的遥感图像应用于土地覆盖分类和地物提取，提高分类及地物提取精度。

模型跨区域和跨传感器超分辨结果分析

基于广东高分1号数据集上训练的ISRGAN超分辨模型，我们分别迁移到新疆高分1号数据集、新疆Landsat8数据集上进行模型的跨区域，跨传感器测试。测试部分结果分别如图2.1.2~图2.1.4所示。

研究区域

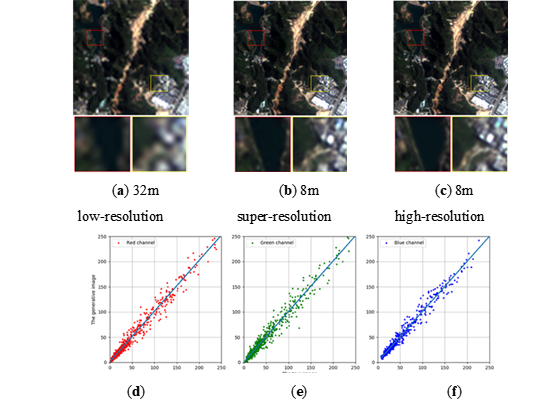
图 2.1.2在广东训练完成的ISRGAN模型在广东本地GF1数据集超分辨率测试结果（a）输入的图像；（b）超分辨图像；（c）地面真值；（d）（e）（f）分别表示超分辨图像真实图像在红、绿和蓝三波段1:1灰度图，斜率分别为1.0063，1.0032和0.9955。

研究区域

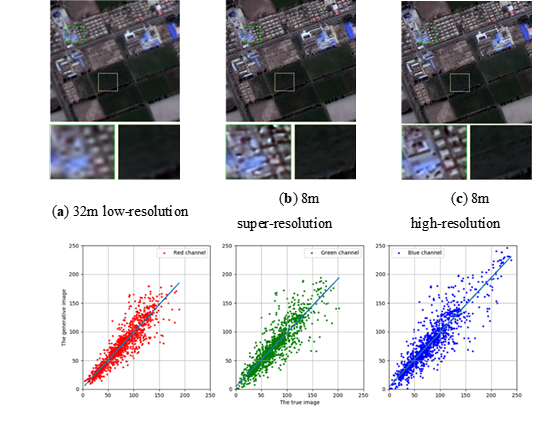
图 2.1.3模型跨区域检验：在广东训练完成的ISRGAN模型直接迁移到新疆GF1数据集超分辨率测试结果（a）输入的图像；（b）超分辨图像；（c）地面真值；（d）（e）（f）分别表示超分辨图像真实图像在红、绿和蓝三波段1:1灰度图，斜率分别为0.9658，0.9378和0.9485。

研究区域

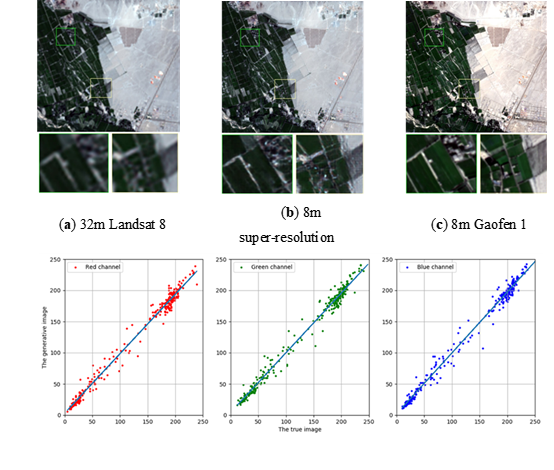
图2.1.4模型跨传感器检验：将广东训练完成的ISRGAN模型在直接迁移到新疆Landsat数据集的超分辨率测试结果（a）输入的图像；（b）超分辨图像；（c）地面真值；（d）（e）（f）分别表示超分辨图像真实图像在红、绿和蓝三波段1:1灰度图，斜率分别为0.9527，0.9564和0.9760。

与传统超分辨模型对比试验

本文主要对比了超分辨领域经典方法领域嵌入法及稀疏表达法，根据相应的超分辨结果，计算其与原始图像的定量化指标，在本文中，由于同一时间同一场景下的Landsat8卫星数据和高分一号卫星数据很难获取，而且其对应的像元个数不一致，考虑到后续在验证模型在跨区域和跨传感器上的普适性上计算标准的一致性，故本文的所有定量计算的参考影像均为超分辨之前的原始影像，计算方法为将超分辨后的影像进行相应的降采样处理，再计算其与原始影像的量化指标。图2.1.5展示了本文基于ISRGAN方法和领域嵌入法、稀疏表达法及SRGAN在3个测试集中测试的部分对比结。

研究区域

结论

本文以生成对抗网络在计算机视觉中的超分辨算法为基础，针对生成对抗网络在训练时存在的梯度消失和模式崩坏等问题，结合WGAN中提出的最小化Wasserstein距离的方法，对原始超分辨网络（SRGAN）进行了改进，提出了ISRGAN网络，并将其应用于遥感影像超分辨。主要结论如下：

1）本文提出的ISRGAN超分辨网络，在遥感影像超分辨任务中，定量指标优于领域嵌入法和稀疏表达法等传统方法；

2）通过在广东GF1影像数据上训练的模型直接应用于新疆GF1影像数据，并对两组数据集的超分辨结果进行t检验，验证了模型在跨区域上的普适性；

3）通过在高分1数据上训练的模型直接应用于Landsat8数据，并对超分辨结果进行t检验，验证了模型在跨传感器上的普适性；

4）以土地利用分类和地物提取为例，验证了超分辨影像在分类和提取精度上的显著提升，表明遥感影像超分辨在资源开发、环境监测、灾害研究和全球变化分析等方面具有重要应用价值。

原文链接

Xiong, Y., Guo, S., Chen, J., Deng, X., & Sun, L. (2020). Improved SRGAN for Remote Sensing Image Super-Resolution Across Locations and Sensors. Remote Sensing, 12(1263), 1–22. https://doi.org/10.3390/rs12081263



    Enjoy Reading This Article?

    Here are some more articles you might like to read next:

  • 基于时空融合的MODIS产品降尺度模型-以海表叶绿素为例
  • 面向地表快速变化场景的时空融合的动态神经网络I-USTFM：以地表温度为例
  • 对抗样本噪声的遥感深度学习分类网络模型
  • 快速评估监督学习中常用遥感分类算法的时间效率
  • 基于光学微波特征融合的典型经济作物提取