$$ \newcommand{\bone}{\mathbf{1}} \newcommand{\bbeta}{\mathbf{\beta}} \newcommand{\bdelta}{\mathbf{\delta}} \newcommand{\bepsilon}{\mathbf{\epsilon}} \newcommand{\blambda}{\mathbf{\lambda}} \newcommand{\bomega}{\mathbf{\omega}} \newcommand{\bpi}{\mathbf{\pi}} \newcommand{\bphi}{\mathbf{\phi}} \newcommand{\bvphi}{\mathbf{\varphi}} \newcommand{\bpsi}{\mathbf{\psi}} \newcommand{\bsigma}{\mathbf{\sigma}} \newcommand{\btheta}{\mathbf{\theta}} \newcommand{\btau}{\mathbf{\tau}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bb}{\mathbf{b}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\boldf}{\mathbf{f}} \newcommand{\bg}{\mathbf{g}} \newcommand{\bh}{\mathbf{h}} \newcommand{\bi}{\mathbf{i}} \newcommand{\bj}{\mathbf{j}} \newcommand{\bk}{\mathbf{k}} \newcommand{\bell}{\mathbf{\ell}} \newcommand{\bm}{\mathbf{m}} \newcommand{\bn}{\mathbf{n}} \newcommand{\bo}{\mathbf{o}} \newcommand{\bp}{\mathbf{p}} \newcommand{\bq}{\mathbf{q}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bt}{\mathbf{t}} \newcommand{\bu}{\mathbf{u}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\bA}{\mathbf{A}} \newcommand{\bB}{\mathbf{B}} \newcommand{\bC}{\mathbf{C}} \newcommand{\bD}{\mathbf{D}} \newcommand{\bE}{\mathbf{E}} \newcommand{\bF}{\mathbf{F}} \newcommand{\bG}{\mathbf{G}} \newcommand{\bH}{\mathbf{H}} \newcommand{\bI}{\mathbf{I}} \newcommand{\bJ}{\mathbf{J}} \newcommand{\bK}{\mathbf{K}} \newcommand{\bL}{\mathbf{L}} \newcommand{\bM}{\mathbf{M}} \newcommand{\bN}{\mathbf{N}} \newcommand{\bP}{\mathbf{P}} \newcommand{\bQ}{\mathbf{Q}} \newcommand{\bR}{\mathbf{R}} \newcommand{\bS}{\mathbf{S}} \newcommand{\bT}{\mathbf{T}} \newcommand{\bU}{\mathbf{U}} \newcommand{\bV}{\mathbf{V}} \newcommand{\bW}{\mathbf{W}} \newcommand{\bX}{\mathbf{X}} \newcommand{\bY}{\mathbf{Y}} \newcommand{\bZ}{\mathbf{Z}} \newcommand{\bsa}{\boldsymbol{a}} \newcommand{\bsb}{\boldsymbol{b}} \newcommand{\bsc}{\boldsymbol{c}} \newcommand{\bsd}{\boldsymbol{d}} \newcommand{\bse}{\boldsymbol{e}} \newcommand{\bsoldf}{\boldsymbol{f}} \newcommand{\bsg}{\boldsymbol{g}} \newcommand{\bsh}{\boldsymbol{h}} \newcommand{\bsi}{\boldsymbol{i}} \newcommand{\bsj}{\boldsymbol{j}} \newcommand{\bsk}{\boldsymbol{k}} \newcommand{\bsell}{\boldsymbol{\ell}} \newcommand{\bsm}{\boldsymbol{m}} \newcommand{\bsn}{\boldsymbol{n}} \newcommand{\bso}{\boldsymbol{o}} \newcommand{\bsp}{\boldsymbol{p}} \newcommand{\bsq}{\boldsymbol{q}} \newcommand{\bsr}{\boldsymbol{r}} \newcommand{\bss}{\boldsymbol{s}} \newcommand{\bst}{\boldsymbol{t}} \newcommand{\bsu}{\boldsymbol{u}} \newcommand{\bsv}{\boldsymbol{v}} \newcommand{\bsw}{\boldsymbol{w}} \newcommand{\bsx}{\boldsymbol{x}} \newcommand{\bsy}{\boldsymbol{y}} \newcommand{\bsz}{\boldsymbol{z}} \newcommand{\bsA}{\boldsymbol{A}} \newcommand{\bsB}{\boldsymbol{B}} \newcommand{\bsC}{\boldsymbol{C}} \newcommand{\bsD}{\boldsymbol{D}} \newcommand{\bsE}{\boldsymbol{E}} \newcommand{\bsF}{\boldsymbol{F}} \newcommand{\bsG}{\boldsymbol{G}} \newcommand{\bsH}{\boldsymbol{H}} \newcommand{\bsI}{\boldsymbol{I}} \newcommand{\bsJ}{\boldsymbol{J}} \newcommand{\bsK}{\boldsymbol{K}} \newcommand{\bsL}{\boldsymbol{L}} \newcommand{\bsM}{\boldsymbol{M}} \newcommand{\bsN}{\boldsymbol{N}} \newcommand{\bsP}{\boldsymbol{P}} \newcommand{\bsQ}{\boldsymbol{Q}} \newcommand{\bsR}{\boldsymbol{R}} \newcommand{\bsS}{\boldsymbol{S}} \newcommand{\bsT}{\boldsymbol{T}} \newcommand{\bsU}{\boldsymbol{U}} \newcommand{\bsV}{\boldsymbol{V}} \newcommand{\bsW}{\boldsymbol{W}} \newcommand{\bsX}{\boldsymbol{X}} \newcommand{\bsY}{\boldsymbol{Y}} \newcommand{\bsZ}{\boldsymbol{Z}} \newcommand{\calA}{\mathcal{A}} \newcommand{\calB}{\mathcal{B}} \newcommand{\calC}{\mathcal{C}} \newcommand{\calD}{\mathcal{D}} \newcommand{\calE}{\mathcal{E}} \newcommand{\calF}{\mathcal{F}} \newcommand{\calG}{\mathcal{G}} \newcommand{\calH}{\mathcal{H}} \newcommand{\calI}{\mathcal{I}} \newcommand{\calJ}{\mathcal{J}} \newcommand{\calK}{\mathcal{K}} \newcommand{\calL}{\mathcal{L}} \newcommand{\calM}{\mathcal{M}} \newcommand{\calN}{\mathcal{N}} \newcommand{\calO}{\mathcal{O}} \newcommand{\calP}{\mathcal{P}} \newcommand{\calQ}{\mathcal{Q}} \newcommand{\calR}{\mathcal{R}} \newcommand{\calS}{\mathcal{S}} \newcommand{\calT}{\mathcal{T}} \newcommand{\calU}{\mathcal{U}} \newcommand{\calV}{\mathcal{V}} \newcommand{\calW}{\mathcal{W}} \newcommand{\calX}{\mathcal{X}} \newcommand{\calY}{\mathcal{Y}} \newcommand{\calZ}{\mathcal{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\F}{\mathbb{F}} \newcommand{\Q}{\mathbb{Q}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \newcommand{\nnz}[1]{\mbox{nnz}(#1)} \newcommand{\dotprod}[2]{\langle #1, #2 \rangle} \newcommand{\ignore}[1]{} \let\Pr\relax \DeclareMathOperator*{\Pr}{\mathbf{Pr}} \newcommand{\E}{\mathbb{E}} \DeclareMathOperator*{\Ex}{\mathbf{E}} \DeclareMathOperator*{\Var}{\mathbf{Var}} \DeclareMathOperator*{\Cov}{\mathbf{Cov}} \DeclareMathOperator*{\stddev}{\mathbf{stddev}} \DeclareMathOperator*{\avg}{avg} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\dist}{dist} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\spn}{span} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\codim}{codim} \DeclareMathOperator{\diag}{diag} \newcommand{\PTIME}{\mathsf{P}} \newcommand{\LOGSPACE}{\mathsf{L}} \newcommand{\ZPP}{\mathsf{ZPP}} \newcommand{\RP}{\mathsf{RP}} \newcommand{\BPP}{\mathsf{BPP}} \newcommand{\P}{\mathsf{P}} \newcommand{\NP}{\mathsf{NP}} \newcommand{\TC}{\mathsf{TC}} \newcommand{\AC}{\mathsf{AC}} \newcommand{\SC}{\mathsf{SC}} \newcommand{\SZK}{\mathsf{SZK}} \newcommand{\AM}{\mathsf{AM}} \newcommand{\IP}{\mathsf{IP}} \newcommand{\PSPACE}{\mathsf{PSPACE}} \newcommand{\EXP}{\mathsf{EXP}} \newcommand{\MIP}{\mathsf{MIP}} \newcommand{\NEXP}{\mathsf{NEXP}} \newcommand{\BQP}{\mathsf{BQP}} \newcommand{\distP}{\mathsf{dist\textbf{P}}} \newcommand{\distNP}{\mathsf{dist\textbf{NP}}} \newcommand{\eps}{\epsilon} \newcommand{\lam}{\lambda} \newcommand{\dleta}{\delta} \newcommand{\simga}{\sigma} \newcommand{\vphi}{\varphi} \newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\wt}[1]{\widetilde{#1}} \newcommand{\wh}[1]{\widehat{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\ot}{\otimes} \newcommand{\zo}{\{0,1\}} \newcommand{\co}{:} %\newcommand{\co}{\colon} \newcommand{\bdry}{\partial} \newcommand{\grad}{\nabla} \newcommand{\transp}{^\intercal} \newcommand{\inv}{^{-1}} \newcommand{\symmdiff}{\triangle} \newcommand{\symdiff}{\symmdiff} \newcommand{\half}{\tfrac{1}{2}} \newcommand{\mathbbm}{\Bbb} \newcommand{\bbone}{\mathbbm 1} \newcommand{\Id}{\bbone} \newcommand{\SAT}{\mathsf{SAT}} \newcommand{\bcalG}{\boldsymbol{\calG}} \newcommand{\calbG}{\bcalG} \newcommand{\bcalX}{\boldsymbol{\calX}} \newcommand{\calbX}{\bcalX} \newcommand{\bcalY}{\boldsymbol{\calY}} \newcommand{\calbY}{\bcalY} \newcommand{\bcalZ}{\boldsymbol{\calZ}} \newcommand{\calbZ}{\bcalZ} $$

对抗样本噪声的遥感深度学习分类网络模型

Created in April 18, 2024 by Shanxin Guo

2024   ·   machine-learning   remote-sensing

post.cover
深圳北站

研究背景

深度学习方法的性能主要取决于两个因素：训练数据量的大小和标签标注的准确性。相比于数据量不足的问题，标签标注噪声问题更难解决。在遥感数据集中，标签噪声普遍存在，主要原因包括以下几点：一是遥感图像的土地类型复杂，需要专业知识才能准确标注；二是多个专家对同一图像标注时可能存在不一致；三是低成本的自动化标注或非专业人员标注往往导致标注结果不可靠。标签噪声会通过影响网络的损失值，使网络参数朝错误方向更新，从而降低分类性能。

针对标签噪声问题的处理方法主要分为两类：一类是针对标签本身，另一类是针对损失值。针对标签的处理方法包括样本筛选和噪声转移矩阵的计算。样本筛选方法通过选择干净样本进行训练，避免噪声样本对网络的负面影响。噪声转移矩阵方法则通过估计类别间的转换概率，纠正噪声标签为干净标签。然而，这些方法的效果依赖于样本选择策略或噪声分布的准确性。

针对损失值的处理方法包括设计鲁棒性损失函数和对损失值赋权重。鲁棒性损失函数通过减少噪声样本对损失值的影响，提高网络的抗噪性能，但在复杂数据集上表现有限。赋权重的方法通过调整样本的损失权重，降低噪声样本的影响，同时提高干净样本的权重，从而提升网络性能。

在遥感图像分类任务中，标签噪声问题的研究较少。为此，本文提出了一种通用的抗噪声网络框架——Weight Loss Net（WLN），通过结合注意力机制动态调整样本权重，降低噪声样本的影响，并在公开数据集上验证了其有效性。

数据源及覆盖区域

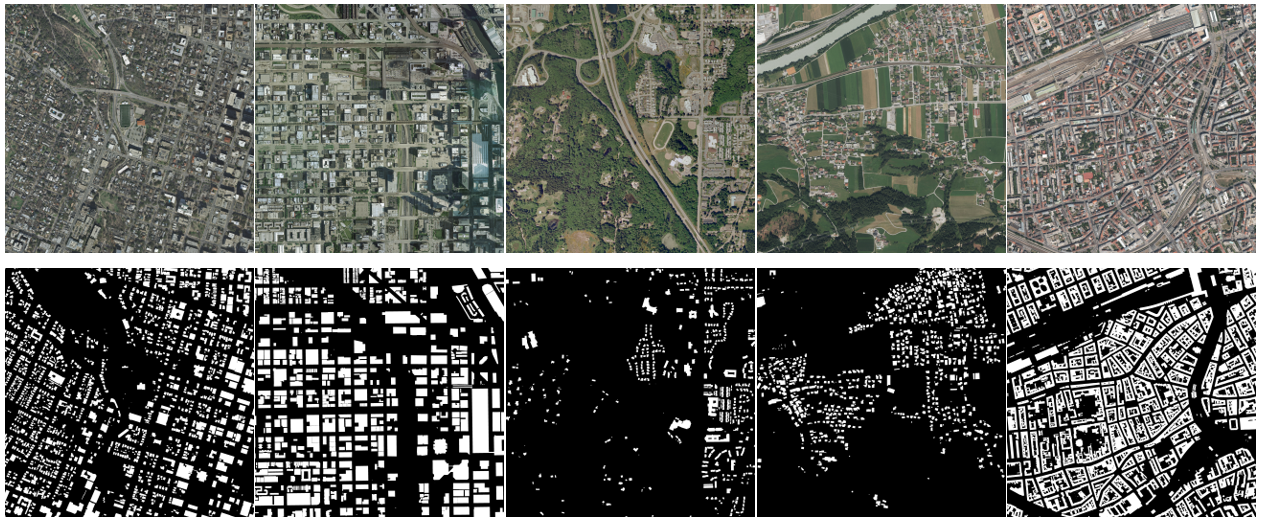
本文采用了Inria Aerial Image Labeling Dataset（以下简称Inria数据集）作为实验数据源。该数据集解决了遥感领域中航空图像像素级自动标注的问题，图像分辨率为30cm，标签分为建筑类别和非建筑类别。数据集覆盖了不同城市区域，包括建筑物密集的大城市和建筑物稀少的小镇。

Inria训练数据集包含180幅5000×5000大小的图像，覆盖Austin、Chicago、Kitsap County、Western Tyrol和Vienna五个地区，总面积为405平方公里。标签由180张单通道图像组成，其中255表示建筑类别，0表示非建筑类别。由于测试集标签不可用，本文将原训练集按8:1:1的比例划分为训练集、验证集和测试集，三者相互独立且不重叠。

研究区域

实验噪声设置

标签噪声是指实例的标注类别与实际类别不一致。在像素级遥感土地覆被标注中，常见的标签噪声包括：1）多标注噪声，标签面积大于实际面积；2）少标注噪声，标签面积小于实际面积；3）错标注噪声，将对象标注为错误类别；4）漏标注噪声，对象的标签完全缺失。

为了模拟标签噪声，本文采用卷积核对标签进行图像膨胀和腐蚀操作。膨胀操作模拟多标注噪声和错标注噪声，腐蚀操作模拟少标注噪声和漏标注噪声。根据卷积核大小，设置了三个噪声等级：卷积核为9表示Noise level 1，卷积核为17表示Noise level 2，卷积核为25表示Noise level 3。此外，设置了五个噪声率（0%、25%、35%、45%、50%）以测试网络在不同噪声水平下的表现。

四种噪声标签的图像

WLN 网络结构

WLN的网络结构图

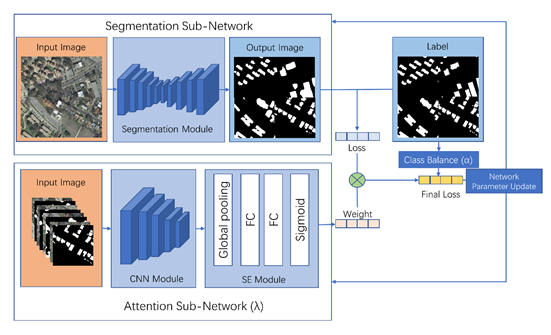
WLN网络由分割子网络和注意力子网络组成。分割子网络用于生成分割结果并计算损失值；注意力子网络通过注意力机制计算样本的损失权重值。为解决腐蚀噪声中类别失衡的问题，本文引入类别平衡系数，与损失值和损失权重值结合，作为最终损失值，用于反向传播更新网络参数。

分割子网络采用U-Net模型，也可替换为其他分割模型。注意力子网络采用SE模块，通过捕获特征通道间的依赖性，为每个通道分配权重，从而增强有用特征，抑制无用特征。

实验结果及分析

实验通过对WLN和U-Net模型在不同噪声类型和水平下的表现进行定量和定性分析，验证了WLN的抗噪性能。

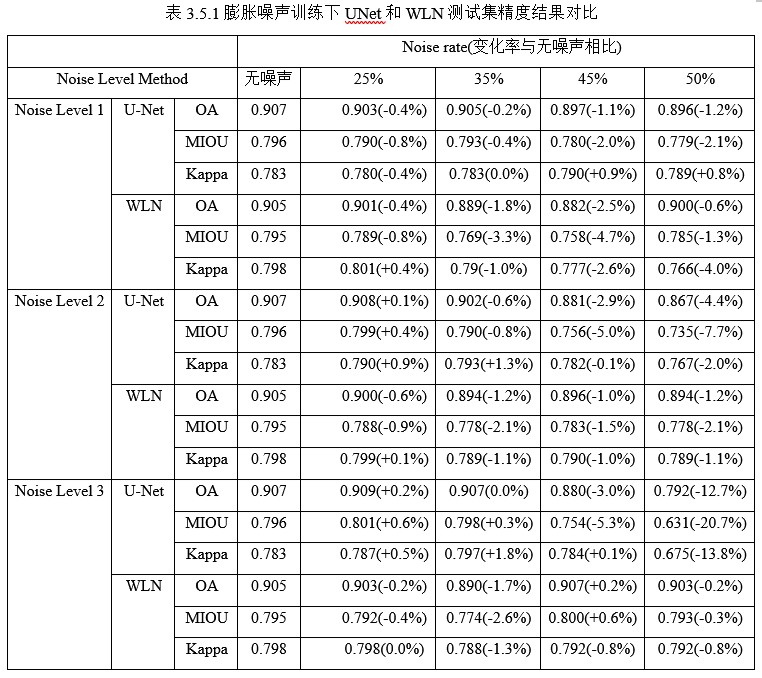
（1）膨胀噪声

在膨胀噪声下，随着噪声率和噪声等级的增加，U-Net的精度显著下降，而WLN能够保持较高的精度。例如，在Noise level 3和噪声率为50%时，U-Net的OA下降12.7%，而WLN仅下降0.2%。

膨胀噪声下的精度曲线

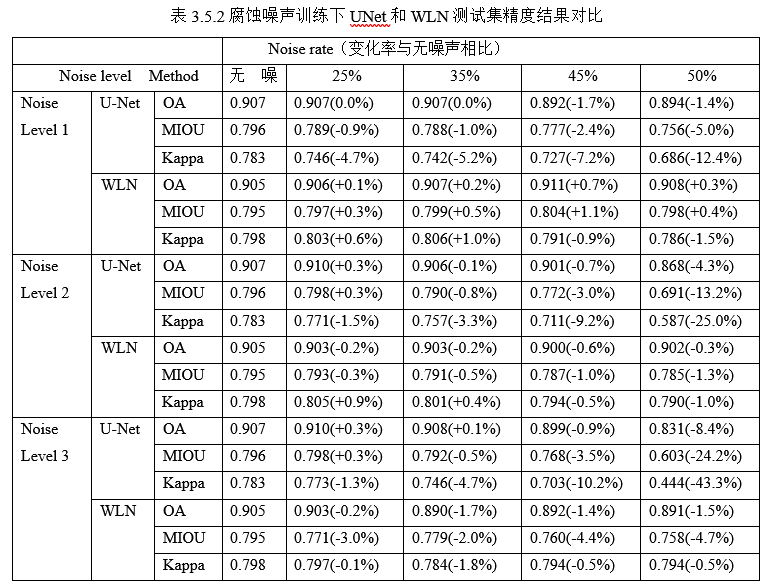
（2）腐蚀噪声

在腐蚀噪声下，U-Net在高噪声率和高噪声等级时表现较差，而WLN的稳定性更好。例如，在Noise level 3和噪声率为50%时，U-Net的OA下降8.4%，而WLN仅下降1.5%。

腐蚀噪声下的精度曲线

提取细节比较

通过目视解译，WLN在膨胀和腐蚀噪声下的地物提取细节明显优于U-Net，尤其是在高噪声水平下，WLN能够更准确地识别建筑物边界。

膨胀噪声类型下U-Net和WLN的提取结果图
腐蚀噪声类型下U-Net和WLN的提取结果图

结论

本文提出了一种通用的抗噪声网络框架WLN，通过结合分割子网络和注意力子网络，有效降低了标签噪声对遥感图像分类的影响。实验结果表明，WLN在不同噪声类型和水平下均表现出较高的精度和鲁棒性，优于传统方法。未来工作将进一步研究类别平衡系数的优化及其在其他任务中的应用。

原文链接

Lin, C., Guo, S., Chen, J., Sun, L., Zheng, X., Yang, Y., & Xiong, Y. (2021). Deep Learning Network Intensification for Preventing Noisy-Labeled Samples for Remote Sensing Classification. Remote Sensing, 13(1689), 1–19.



    Enjoy Reading This Article?

    Here are some more articles you might like to read next:

  • 基于时空融合的MODIS产品降尺度模型-以海表叶绿素为例
  • 面向地表快速变化场景的时空融合的动态神经网络I-USTFM：以地表温度为例
  • 快速评估监督学习中常用遥感分类算法的时间效率
  • 基于光学微波特征融合的典型经济作物提取
  • 基于对抗神经网络ISRGAN的多源遥感数据融合与超分辨模型